che può essere interpretata come una assegnazione mediante la quale la variabile a assume il valore del rapporto tra le variabili F e m. Se necessario, il docente dovrà sottolineare la distinzione tra il concetto di assegnazione e la più familiare relazione di uguaglianza. A questo proposto, non è superfluo ricordare come alcuni linguaggi di programmazione rendano tale distinzione esplicita, ricorrendo a simboli diversi per i due concetti (vedi Pascal).
In Excel, possiamo considerare le celle come variabili e le formule come istruzioni di assegnazione. Ad esempio, vediamo come la formula appena considerata possa essere rappresentata nel foglio di calcolo:

	A	B	C	D
1	Accelerazione	Forza	Massa
2	=B2/C2	12	2
3
4

Nella figura riportata qui sopra, le celle A2, B2 e C2 possono essere viste come altrettante variabili. In particolare, possiamo immaginare che le celle B2 e C2 contengano, rispettivamente, il valore della forza applicata ad un punto e la massa del punto stesso. Se vogliamo che la corrispondente accelerazione compaia in A2, dovremo allora assegnare il valore B2/C2 alla variabile A2. A questo scopo, basterà inserire nella cella la formula "=B2/C2" e confermare con invio; in A2 comparirà immediatamente il risultato voluto, come illustrato nella figura seguente. Modificando i valori delle variabili B2 e C2, il dato in A2 viene aggiornato automaticamente.

	A	B	C	D
1	Accelerazione	Forza	Massa
2	6	12	2
3
4

Attività 2: Istruzioni con riferimenti circolari

Obiettivi:
- Comprendere il significato delle istruzioni con riferimenti circolari
- Essere in grado di impostare una istruzione con riferimento circolare in Excel

Dopo aver richiamato il concetto di istruzione di assegnazione, l'insegnante propone agli allievi una espressione del tipo

t = t + 1

ed avvia una breve discussione sulle sue possibili interpretazioni. Se il simbolo "=" viene inteso come relazione di uguaglianza, la formula appare poco significativa (equazione impossibile); al contrario, se lo stesso simbolo viene inteso come "operatore di assegnazione", l'espressione corrisponde ad una chiara prescrizione:

1. si calcola il valore del membro destro dell'assegnazione, utilizzando il valore di t presente in memoria
2. il valore così calcolato viene quindi attribuito alla variabile t.

Nel nostro caso, se il valore di t presente in memoria fosse t=4, l'esecuzione dell'istruzione lo modificherebbe in t=5.
I linguaggi di programmazione di tipo imperativo seguono proprio la prescrizione appena descritta, anche se possono differenziarsi per la sintassi dell'istruzione (ad esempio in Pascal si utilizza il simbolo ":=" come operatore di assegnazione).

Il passo successivo consiste nel mostrare come predisporre un foglio elettronico in modo che esso interpreti le istruzioni con riferimenti circolari.

Immaginiamo allora che la variabile t sia associata alla cella A1. Ricordando la corrispondenza tra istruzioni di assegnazione e formule, sarà necessario digitare nella stessa cella A1 il testo "=A1+1", come indicato nella figura seguente.

	A	B	C	D
1	=A1+1
2
3
4

Fatto questo, è necessario informare Excel che intendiamo interpretare l'istruzione in modo analogo a quanto accade nei linguaggi di programmazione di tipo imperativo. A questo scopo è necessario agire su alcune impostazioni del programma:

- dal menu Strumenti selezionare la voce Opzioni
- attivare la scheda Calcolo
- spuntare la voce Iterazioni
- impostare a 1 il numero massimo di iterazioni

Per verificare l'effetto delle nuove impostazioni inseriamo nella cella A1 la formula "=A1+1" e digitiamo invio. In A1 dovrebbe comparire il numero 1, in quanto il valore delle celle è inizializzato a zero. Per eseguire più volte l'istruzione di assegnazione basterà premere ripetutamente il tasto F9 (il tasto F9 determina l'aggiornamento dei valori inseriti nelle celle); ad ogni pressione il contenuto della cella A1 verrà incrementato di una unità, indicando che l'istruzione di assegnazione A1=A1+1 viene interpretata come desiderato.

Attività 3 - Equazioni del moto in presenza di un campo gravitazionale centrale

Scopo di questa unità didattica è richiamare alcune nozioni fisiche e matematiche che verranno utilizzate nella simulazione del moto gravitazionale. Se necessario, l'insegnante dovrà ricordare che il problema fondamentale della Dinamica consiste in quanto segue:

Prevedere il moto dei punti materiali partendo dalla conoscenza delle cosiddette condizioni iniziali, cioè dalla posizione e dalla velocità dei punti in un particolare istante.

Si presuppone inoltre che il docente abbia spiegato agli alunni come la soluzione delle equazioni del moto possa essere ottenuta attraverso semplici relazioni di ricorrenza, secondo quanto indicato nella scheda per insegnanti allegata.

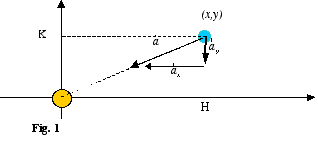Il sistema fisico di cui ci occupiamo è costituito da una massa (pianeta) che orbita attorno ad un centro di forza fisso (stella). Per studiare il moto del pianeta è comodo introdurre un sistema di assi cartesiani con origine nel centro di forze come illustrato in fig. 1. E' opportuno che l'insegnante ribadisca come la posizione del pianeta sia univocamente determinata dalla posizione delle proiezioni H e K sugli assi cartesiani; in altri termini, è importante sottolineare come il moto (piano) del pianeta possa essere analizzato studiando i moti (rettilinei) compiuti da H e K. A questo punto, l'insegnate invita gli studenti a calcolare l'accelerazione delle proiezioni H e K in funzione della posizione del pianeta. Se necessario, il docente suggerisce le semplici considerazioni di similitudine con cui ottenere la risposta. Tenendo presente che l'accelerazione del pianeta ha modulo

,

si ricava

;

Scegliendo opportunamente le unità di misura (Basta assumere come unità di tempo la quantità dove L è l'unità di lunghezza), possiamo fare in modo che il prodotto GM abbia valore unitario; le precedenti relazioni diventano così:

;

Secondo quanto illustrato nella scheda per l'insegnante, la conoscenza delle accelerazioni in funzione della posizione ci consente di determinare il moto del pianeta attraverso quattro relazioni ricorsive:

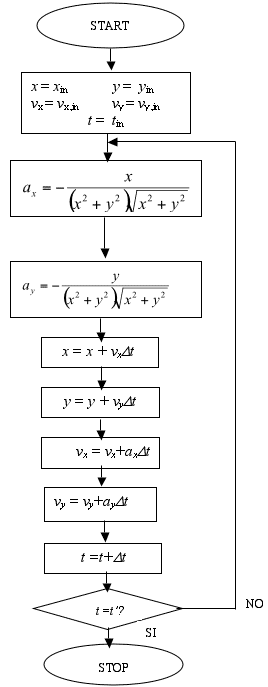
Il significato e l'uso delle precedenti relazioni può forse essere chiarito da un diagramma di flusso, schematicamente riportato in fig. 2

	La prima fase dell'algoritmo consiste nella lettura delle condizioni iniziali, poniamo all'istante t.
	Il programma calcola quindi le accelerazioni ax e ay corrispondenti ai valori della posizione presentata in ingresso.
	Le coordinate del pianeta al tempo t+Dt vengono calcolate utilizzando le prime due relazioni ricorsive.
	Le nuove componenti della velocità vx e vy vengono stimate utilizzando la terza e la quarta relazione.
	La procedura viene iterata sino al raggiungimento del "tempo finale" t' .

Fig. 2

Attività 4 - Soluzione delle equazioni del moto e relativa animazione

L'ultima fase della nostra unità è dedicata alla creazione di un foglio elettronico con cui simulare e visualizzare il moto di un pianeta in presenza di una forza gravitazionale centrale.

Ovviamente, è indispensabile che l'utente possa interagire con il foglio, ad esempio modificando i parametri della simulazione o variando a piacimento le condizioni iniziali del problema. Per far questo utilizzeremo una cella, ad esempio la cella A1, in cui scriveremo il numero 1 per avviare la simulazione, oppure il numero 0 per "inizializzare" il moto.

Sarà poi utile disporre di quattro celle per immettere le condizioni iniziali, cioè la posizione e la velocità del pianeta nell'istante iniziale. Stabiliamo di utilizzare allo scopo le celle B2:B5. In particolare, inseriremo nelle celle B2, B3, B4, B5 rispettivamente l'ascissa iniziale del pianeta, l'ordinata iniziale, la componente lungo x della velocità iniziale, la componente lungo y della velocità iniziale.

Una ulteriore cella, poniamo C1, verrà utilizzata per memorizzare "il passo d'integrazione" Dt utilizzato nelle relazioni di ricorrenza.

	A	B	C	D
1	0	Dt =	0,09	...
2	xiniziale=	1	x(t)=	...
3	yiniziale=	1	y(t)=	...
4	vx iniziale=	0	vx(t)=	...
5	vy iniziale=	1	vy(t)=	...

Altre quattro celle, D2:D5, andranno utilizzate per calcolare le quattro variabili fondamentali del problema cioè le due coordinate x e y che individuano la posizione del pianeta e le componenti cartesiane v_x e v_y della sua velocità.

Focalizziamo ora la nostra attenzione sulla cella D4 e cerchiamo di stabilire la formula da inserire. Dovremo innanzitutto distinguere due casi: il caso in cui A1=0 (inizializzazione del problema) ed il caso in cui A1=1 (simulazione in corso).
Se A1 = 0 , il programma deve limitarsi a copiare in D2 la condizione iniziale inserita in B4; in D4 dovrebbe pertanto comparire la formula "=B4".
Al contrario, se A1 =1, Excel dovrebbe applicare la relazione ricorsiva

che, tenendo conto dei risultati ottenuti nella precedente unità, diventa

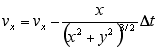
In D4 dovrebbe pertanto comparire la formula "=D4-C1*D4/(D2^2+D3^2)^(3/2)". In definitiva, nella cella F2 vorremmo scrivere una espressione del tipo:

se A1 = 0 allora B4 altrimenti D4-C1*D4/(D2^2+D3^2)^(3/2).

A tale scopo, Excel contempla una struttura di selezione con la seguente sintassi:

SE(A1=0; B4; D4-C1*D4/(D2^2+D3^2)^(3/2))

Una volta chiarito come impostare il contenuto della cella D4, l'insegnante potrebbe lasciare agli studenti il compito di definire il contenuto delle celle D2, D3 e D5:

	A	B	C	D
1	1	Dt =	0,09
2		1	x=	=SE(A1=0; B2; D2+D4*C1)
3		1	y=	=SE(A1=0; B3; D3+D5*C1)
4		0	vx=	=SE(A1=0; B4; D4-C1*D4/(D2^2+D3^2)^(3/2)
5		1	vy=	=SE(A1=0; B4; D5-C1*D5/(D2^2+D3^2)^(3/2)

Per maggiore chiarezza, sottolineiamo la corrispondenza tra le formule inserite nel range D2:D5 e le relazioni di ricorrenza ricavate nell'unità precedente:

• D2 = D2+D4*C1 x = x + v_xDt
• D3 = D3+D5*C1 y = y + v_xDt
• D4 = D4-C1*D4/(D2^2+D3^2)^(3/2) v_x = v_x + a_xDt
• D5 = D4-C1*D4/(D2^2+D3^2)^(3/2) v_v = v_v + a_yDt

Una volta inserite le relazioni di ricorrenza in D2:D5 , il foglio di lavoro è pronto per determinare il moto del pianeta; in particolare, ad ogni pressione del tasto F9, Excel eseguirà i calcoli indicati nelle celle, facendo così avanzare di "un passo" l'evoluzione temporale del sistema, dal tempo t al tempo t+Dt.

Per visualizzare il moto del pianeta con una animazione grafica, basterà semplicemente creare un grafico con un solo punto di coordinate x = D2 e y = D3 (cioè le coordinate del pianeta). Premendo una volta il tasto F9, i valori di tutte le celle vengono aggiornati e vedremo il pianeta compiere un passo della simulazione; tenendo premuto il tasto F9, riceveremo invece l'impressione di un moto continuo.

Ulteriori dettagli relativi alla preparazione del foglio elettronico possono essere desunti dall'esempio che alleghiamo.
La velocità dell'animazione può essere notevolmente aumentata se, per effettuare i calcoli, si utilizza una Macro in luogo del tasto F9 (vedi esempio allegato).

Verifica degli apprendimenti

Vengono assegnati due problemi, il primo da risolversi su supporto cartaceo, il secondo da svolgere al calcolatore. Il tempo a disposizione è di 60 minuti. Per semplicità, nei problemi sono state volutamente omesse le unità di misura.

Problema 1
Un punto materiale di massa M=1 si muove lungo l'asse x ed è soggetto alla forza "elastica" F(x) = -x. All'istante t=0, il punto ha una velocità v(0) = 2 e si trova in x(0) = 3. Assumendo che per intervalli di tempo Dt=1/10 la velocità e l'accelerazione possano ritenersi costanti, rispondere ai seguenti quesiti:

i) determinare la velocità del punto per t = 1/10
ii) determinare la posizione del punto per t = 1/10
iii) utilizzando i valori determinati al punto i) e ii) calcolare la velocità e la posizione della particella per t=2/10.

Problema 2
Predisporre un foglio elettronico che simuli il moto descritto nel problema precedente.

---

Soluzione del Problema 1

i)

ii)

iii) ;

---

Scheda Insegnante – Previsione del moto attraverso equazioni alle differenze finite

Consideriamo un punto materiale che si muove (per semplicità) su una retta e poniamoci il seguente problema:

se conosciamo la posizione e la velocità del punto in un certo istante t, come possiamo calcolare la posizione e la velocità del punto in un istante successivo t+Dt ?

In base alle definizioni stesse di velocità ed accelerazione, valgono le seguenti relazioni:

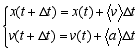
dove <v> e <a> sono la velocità media e l'accelerazione media nell'intervallo di tempo [t, t+Dt]. Se l'intervallo di tempo è sufficientemente piccolo, i suddetti valori medi possono essere rimpiazzati dai valori istantanei della velocità e della accelerazione al tempo t:

Se, inoltre, l'accelerazione è una funzione della posizione e della velocità (questo in sostanza è il reale contenuto della seconda legge della dinamica), le precedenti relazioni diventano

In definitiva si osserva che la posizione e la velocità al tempo t determinano univocamente la posizione e la velocità al tempo t+Dt; a questo punto, i nuovi valori delle grandezze x e v possono essere inserite nei membri destri delle equazioni, ottenendo in questo modo la posizione e la velocità al tempo t+2Dt. Iterando più volte la stessa procedura possiamo, in linea di principio, determinare la posizione del punto in qualunque istante t' successivo (o precedente) t.

[inizio del testo] [indice]