![]() e
e ![]()
Disciplina: fisica
Docente: Alessandra Mossenta
A conclusione della sottounità si vorrebbe aver stimolato negli allievi una riflessione che si può sintetizzare in quanto segue.
Le rappresentazioni grafiche di un processo fisico ottenute con il calcolatore costituiscono un potente mezzo comunicativo, da usare però in modo critico. Un uso consapevole di questi strumenti presuppone non solo che sia possibile interpretare le rappresentazioni più astratte (ad esempio, i grafici cartesiani) ma anche che siano noti i processi che sottostanno alla rappresentazione, almeno nelle loro linee generali, così da poterli adattare alle proprie esigenze. L'intervento dell'utente del programma nel fornire dati adeguati alla realtà di cui si crea un modello visuale può produrre rappresentazioni coerenti con essa; un'utilizzazione priva di riscontri non ha la validità conoscitiva che un programma come Interactive Physics (IP) potrebbe fornire, anche in virtù della rappresentazione della realtà fenomenologica che propone, quasi "fotografica".
Per raggiungere l'obiettivo viene presentato il modo in cui è possibile rappresentare, attraverso il programma di modellizzazione IP (che utilizza simulazioni numeriche) un'esperienza di laboratorio, portata avanti in precedenza mediante un sistema di acquisizione dati in linea con l'elaboratore. L'esperienza scelta permette di mettere in evidenza anche la rilevanza degli strumenti di calcolo per fornire soluzioni delle equazioni del moto non ottenibili per via analitica.
La metodologia prescelta prevede di proporre agli allievi una lezione frontale presentando agli allievi le simulazioni ottenute con il programma Interactive Physics e operando con esse; non verrà eseguita con la classe l'esperienza in laboratorio a cui ci si riferisce, per ragioni di tempo.
Nella sottounità del prof. Ragazzon si illustra la capacità del programma Excel per ottenere soluzioni numeriche delle equazioni del moto sviluppate a partire dalla meccanica newtoniana. In questa sottounità si cerca di dare un'idea della portata di un simile problema nell'ambito della descrizione della fenomenologia fisica fornita dalla visione newtoniana, e quindi dei contributi e dei limiti derivanti dall'utilizzo, per lo studio di un fenomeno, di un programma (Interactive Physics) che privilegia il canale visivo per raffigurare l'evoluzione del fenomeno, sulla base della metodologia già vista nella precedente sottounità. Contestualmente si analizzeranno pure diverse modalità di rappresentazione visiva di fenomeni fisici.
Prerequisiti
- Conoscere la legge fondamentale della dinamica e le rappresentazioni cartesiane delle leggi orarie più comuni.
- Saper utilizzare Excel, e possibilmente anche il programma Interactive Physics (IP).
Obiettivi
Lo sviluppo dell'unità dovrebbe consentire di:
- Distinguere tra tipi diversi di rappresentazione iconica dello spazio fisico, individuarne le peculiarità e valutarne la potenzialità, in particolare in relazione alla efficacia comunicativa.
- Distinguere la modalità di rappresentazione dell'informazione dall'informazione in sé.
- Comprendere il ruolo ricoperto dal calcolatore e quello dell'utente nello sviluppo di una simulazione.
- Comprendere il legame tra la rappresentazione fornita dal programma e il fenomeno reale.
- Comprendere la valenza conoscitiva di un processo di modellizzazione relativamente al modello newtoniano.
Metodologia
Lezione frontale con relazione dei processi messi in atto su un esperimento reale (1).
Utilizzo dei programmi Excel, Interactive Physics (2), Science Workshop (3).
Come precedentemente precisato, la modalità prescelta è quella della lezione frontale con la classe, utilizzando un calcolatore con videoproiettore su cui sia installato il programma Interactive Physics. Si prevede di condurre la lezione sviluppando i seguenti punti:
1) La legge fondamentale della dinamica permette di determinare facilmente la posizione che un oggetto avrà dopo un certo tempo dall'inizio dell'osservazione solo nel caso in cui la forza sia costante: in caso contrario, la determinazione della posizione finale del corpo presenta aspetti problematici: questa conclusione scaturisce da un'analisi, su un caso particolare, dei problemi connessi con la risoluzione dell'equazione F = ma e con la conseguente determinazione della posizione finale di un oggetto.
2) L'equazione può essere risolta con metodi numerici: si illustra quindi il metodo di risoluzione più semplice.
3) I calcoli connessi potranno essere portati a termine da un calcolatore, a cui sia stato fornito un programma per tale calcolo, in sé non complesso: il calcolatore viene utilizzato come macchina calcolatrice.
4) I risultati ottenuti danno le posizioni assunte dal corpo nel tempo, e possono essere fornite sia come elenco numerico, sia come rappresentazione grafica nello spazio cartesiano, s(t), sia come rappresentazione "fedele" dello spazio fisico in una simulazione (forse, meglio, modellizzazione). Si può osservare che la rappresentazione dell'andamento della posizione nel tempo in un diagramma cartesiano costituisce a sua volta un linguaggio (di tipo grafico) simbolico, nella misura in cui ad ogni curva del piano cartesiano si riesce ad associare una situazione fisica reale, nello spazio euclideo. La rappresentazione attraverso le immagini degli oggetti è la più semplice da interpretare; inoltre, è dinamica. Potremmo indicare con il termine "analogico" il tipo di linguaggio utilizzato in tali animazioni.
5) Esame delle potenzialità di due programmi utili a fornire le soluzioni cercate: un programma come Excel è in grado sia di effettuare i conti sia di darne una rappresentazione numerica o grafica; la struttura delle operazioni compiute è abbastanza evidente. Un programma come IP è in grado di rappresentare, in particolare, la parte "figurativa" della rappresentazione e, sebbene la struttura delle operazioni compiute per conseguire le rappresentazioni sia nascosta, essa è presente pure in IP.
6) L'interfaccia visuale di IP comporta comunque che l'utente fornisca istruzioni determinanti alla macchina: si devono comunicare delle ipotesi sulla natura del sistema che si vuole trattare (ad esempio, quale tipo di forza sarà applicata al corpo) che esso utilizzerà come dati iniziali da cui far partire i calcoli; si deve scegliere il tipo di metodo numerico usato per effettuare i calcoli e i relativi parametri (in particolare, l'intervallo di integrazione).
7) La rappresentazione che si ottiene per il movimento del corpo dipende dalle impostazioni fornite alla macchina e dalle ipotesi sul sistema, comunicate anche in modo implicito; solo il confronto con il fenomeno reale permette di stabilire quale, tra le ipotesi, è la più adatta alla sua descrizione.
Si riporta il testo della lezione che si intende proporre agli allievi.
I parte (1 ora)
N.B. Le considerazioni che seguono riguardano solo i moti in una dimensione. Non si farà quindi uso di notazione vettoriale.
Le leggi della Meccanica consentono di ottenere delle "previsioni"
relativamente al moto dei corpi, nel senso che danno la possibilità di
stabilire dove si troverà un certo corpo a un determinato istante t,
o, che è lo stesso, quando esso si troverà in una determinata
posizione, e con quale velocità. Per la fisica classica il problema è
risolubile purché si conoscano posizione e velocità del corpo
a un certo istante (quello da cui inizia l'osservazione) e le forze che agiscono
su di esso. Tuttavia la soluzione delle equazioni del moto è semplice
solo in pochi casi. E' possibile trovare un legame espresso
da funzioni matematiche elementari tra tempo e posizione (o tra tempo e
velocità) solo nel caso che il corpo si muova con velocità costante
o con accelerazione costante. Dato il legame espresso dalla seconda legge della
dinamica tra l'accelerazione e la forza totale che agisce sul corpo, questa
condizione diventa quella per cui deve essere nulla o costante la forza stessa.
E' quindi rilevante chiedersi come affrontare il problema se la forza non è costante.
Per capire l'ampiezza del problema esaminiamo un esempio in cui la forza non si mantiene costante: è noto come l'espressione più semplice della forza elastica in una molla allungata sia F=-kx, ove con k si indica la costante elastica e con x l'allungamento subito dalla molla. Immaginiamo di aver allungato una molla orizzontale, vincolata ad una estremità e con una massa all'estremo libero, in condizioni di assenza di attrito, e quindi di lasciare la presa: da quest'istante la molla subirà l'azione di richiamo dovuta alla forza elastica. Poiché lungo il tragitto l'allungamento della molla diventerà via via più piccolo, anche il valore della forza varierà. La massa sarà quindi soggetta a una forza variabile, che diventerà nulla quando la molla raggiungerà la posizione d'equilibrio. L'esercizio che segue permette avere un'idea di come il valore della forza muti nel tempo.
Esercizio: Supponiamo di avere una molla con k pari a 0,02 N/cm; supponiamo che sia stata allungata di 5 cm e quindi rilasciata. Calcoliamo quanto vale la forza elastica quando l'allungamento è massimo e ad ogni diminuzione di un centimetro, finché l'allungamento diviene 0. Riempiamo la tabella con i risultati.
| Allungamenti | x=5cm | x=4cm | x=3cm | x=2cm | x=1cm | x=0cm |
| Forza elastica (in modulo) |
Se la forza è variabile lo sarà anche l'accelerazione, e dunque per ricavarsi posizione e velocità della massa attaccata alla molla non è possibile utilizzare nessuna delle leggi orarie più semplici: né quella con accelerazione nulla né quella con accelerazione costante.
Sebbene in questo semplice esempio sia possibile ricavare le equazioni che forniscono i valori della posizione e della velocità a qualunque istante (noti che siano posizioni e velocità iniziali, come sopra), con procedimenti matematici affrontabili in classi liceali, non sempre questi possono essere usati per ricavare analiticamente l'equazione del moto. In tal caso si ricorre a metodi numerici; uno dei più semplici è il metodo d'integrazione di Eulero, che verrà preso in esame in questa lezione.
L'intervallo di tempo in cui si vuole studiare il moto viene suddiviso in intervallini di ampiezza costante, indicata con Dt. Per ogni intervallo si calcola dapprima il valore della forza nell'istante iniziale, quindi, dividendo quest'ultima per la massa del corpo considerato, si ottiene l'accelerazione; si usano poi le leggi del moto per determinare la velocità e la posizione all'istante finale dell'intervallo, valori che diverranno quelli iniziali per l'intervallo seguente. In simboli, si ha:
![]() e
e ![]()
ove le accelerazioni nei diversi istanti sono determinate dalle forze presenti all'inizio di ogni intervallo.
L'esercizio seguente, già svolto, illustrerà il procedimento descritto (4).
Esercizio: Immaginiamo di essere interessati a un corpo, di massa pari a 2,5 Kg, che è soggetto ad una forza crescente nel tempo secondo la legge F = 2t. Calcoliamo quale sarà la posizione del corpo, partito dalla posizione 0 con velocità nulla, dopo 5 secondi. Scegliamo un Dt pari a 1 secondo.
| t (s) | F(N) | a(m/s/s) | v(m/s) | x(m) |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 0,8 | 0,8*1+0=0,8 | 0 |
| 2 | 4 | 1,6 | 1,6*1+0,8=2,4 | 0+0,8*1=0,8 |
| 3 | 6 | 2,4 | 2,4*1+2,4=4,8 | 0,8+2,4*1=3,2 |
| 4 | 8 | 3,2 | 3,2*1+4,8=8,0 | 3,2+4,8*1=8,0 |
| 5 | 10 | 4 | 4*1+8,0=12 | 8,0+8,0*1=16 |
A questo punto bisogna sottolineare due cose. La prima è che non esiste
un solo metodo per ricavarsi le accelerazioni necessarie al calcolo; metodi
diversi risultano più o meno accurati nella produzione dei valori che
risultano da ciascun passo. Inoltre bisogna sottolineare il fatto che ogni metodo
risente come fattore critico dell'ampiezza dell'intervallo Dt:
minore sarà questa, maggiore l'accuratezza del calcolo, ma anche maggiore
il numero di passi necessario per compiere la simulazione e quindi più
lunghi i tempi per il calcolo.
L'esercizio che segue dà un'idea dell'effetto che si ottiene cambiando
l'intervallo di tempo.
Esercizio: Ripeti la procedura precedente, ma con Dt pari a 0,5 secondi.
| t (s) | F(N) | a(m/s/s) | v(m/s) | x(m) |
| 0 | ||||
| 0,5 | ||||
| 1 | ||||
| 1,5 | ||||
| 2 | ||||
| 2,5 | ||||
| 3 | ||||
| 3,5 | ||||
| 4 | ||||
| 4,5 | ||||
| 5 |
I dati ottenuti, riportati via via nella tabella, si possono confrontare con quelli della tabella precedente. Come lavoro domestico si sottolineeranno in questa tabella i valori diversi rispetto alla precedente.
Per gestire la mole di calcoli relativi a queste simulazioni il computer diventa prezioso. A conclusione del procedimento di calcolo si avranno tante coppie di dati (x, t) quanti gli intervalli più uno; altrettante saranno le coppie (v, t).
Vediamo come l'esercizio considerato possa essere affrontato utilizzando il foglio elettronico Excel. Sarà necessario essere in grado di far eseguire i conti al programma (attivando una modalità esecutiva di funzioni predefinite), ma anche scrivere, con il linguaggio proprio del programma, le istruzioni di calcolo che, eseguite dalla macchina, produrranno i valori richiesti all'uscita. Queste istruzioni sono scritte esplicitamente, e racchiudono le ipotesi fatte sul sistema che ci interessa (nel caso dell'esempio, i dati del problema). Anche se nell'esempio visto ci sono dati numerici e operazioni elementari, con questo tipo di programmi si possono effettuare operazioni decisamente più complesse, per ottenere un "risultato" scritto in una cella. Al termine dell'elaborazione dei dati avremo sullo schermo una tabella, in cui verranno scritti i valori numerici che ci interessano.
Esercizio (per casa): Scrivi con il programma Excel la procedura che permette di ottenere lo stesso risultato del calcolo "manuale" visto sopra.
Rapida sintesi della lezione precedente, riprendendo i punti 1, 2, 3 della scaletta descritta in "Sviluppo della sottounità".
Il programma Excel oltre a realizzare calcoli consente di rappresentare dati in modo grafico. Nel caso dell'esempio, sarà possibile costruire due grafici cartesiani (diagrammi orari), quello della posizione in funzione del tempo e quello della velocità in funzione del tempo. I diagrammi orari non sono "riproduzioni" della situazione concreta sotto esame, ma modalità di rappresentazione dei dati numerici che presentano il vantaggio, rispetto alle tabelle di dati, di evidenziare in modo efficace i legami tra le diverse grandezze fisiche in gioco nella situazione considerata. Le informazioni che si possono ricavare rapidamente da un grafico sono spesso "invisibili" in una tabella. Tuttavia bisogna sottolineare come questo vantaggio sia subordinato alla capacità, in chi guarda il grafico, di interpretare la curva che vede: è necessario riuscire ad associare ad ogni curva del piano cartesiano una situazione fisica concreta, nello spazio euclideo. Non è forse superfluo sottolineare come un'interpretazione errata del significato dell'immagine porta dietro un totale fraintendimento rispetto alla natura del sistema descritto: la modalità visiva, più efficace, subordina le sue potenzialità alla convenzione rispetto al significato che vuole assumere.
A questo punto può essere interessante, per riflettere sul rapporto tra la modalità descrittiva dei diagrammi cartesiani e la situazione descritta, prendere in esame una piccola esperienza (5), effettuata in laboratorio con le seguenti modalità:
Un carrello viene fatto correre su una guida a basso attrito. Un sensore collegato al computer rileva ad intervalli regolari la posizione dell'oggetto, con un dispositivo del tipo dei sonar che si utilizzano nei sottomarini. Il segnale acquisito viene convertito dal calcolatore stesso in un valore di distanza (per esempio, attraverso un programma, che in questo caso è Science Workshop).
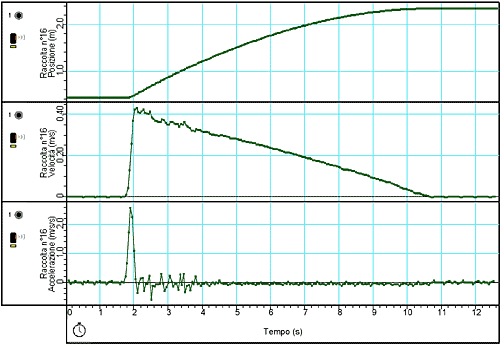
I dati relativi all'esperimento possono essere rappresentati sotto forma di tabella o sotto forma di grafico, come illustrato nella figura seguente. In questo caso il calcolatore può operare sui dati acquisiti e fornire dei valori per grandezze derivate (nel nostro caso, velocità e accelerazione), con una procedura predefinita attivabile dall'utente.
La convenzione che sta alla base della rappresentazione grafica delle leggi orarie ci dice che nessuno dei tre grafici rappresenta (nel senso di indicarla in scala) la traiettoria, rettilinea, del carrello. Per rappresentare la traiettoria in questo senso si utilizzerà lo stesso strumento (il piano cartesiano) ma come strumento di costruzione di un sistema di riferimento, in cui il valore dei dati è quello di coordinata spaziale.
E' possibile ottenere però rappresentazioni dei dati più "realistiche" rispetto a quelle in forma di grafico: le simulazioni. Un programma apposito per simulazioni fisiche è Interactive Physics, che permette di rappresentare sullo schermo l'evoluzione temporale di sistemi prescelti dall'utente. E' il caso di fare qualche osservazione su come si presenta lo schermo all'apertura del programma (6): ciò che si ha davanti è inteso essere una rappresentazione dello spazio su cui possono essere collocati oggetti. Per effettuare questa operazione è sufficiente selezionare un oggetto e collocarlo, con il click del mouse, nello "spazio". Se viene attivata la simulazione vediamo il corpo cadere, proprio come lo vedremmo cadere se fosse sospeso nell'aria intorno a noi (sorgente IP). I sistemi fisici vengono rappresentati mediante figure in forma di poligoni o di circonferenze o ellissi. La rappresentazione degli oggetti con queste figure consente di concentrare l'attenzione sulle caratteristiche salienti dei corpi, mettendo in secondo piano ciò che risulta irrilevante ai fini della modellizzazione. La modalità figurativa non viene usata soltanto per rappresentare oggetti, ma anche le azioni che vengono compiute su di essi, mediante icone. Se desideriamo far agire una forza su un corpo utilizzeremo un'apposita icona associata alla forza. Si può notare come accanto a rappresentazioni di oggetti concreti possano essere realizzate rappresentazioni di enti astratti; mentre i primi, tuttavia, risultano facilmente comprensibili nei loro significati, i secondi hanno bisogno di maggior esplicitazione, chiaramente sulla base di convenzioni: così l'icona della molla, ad esempio, simboleggia l'applicazione di una forza di tipo elastico tra due corpi.
L'interfaccia grafica indubbiamente facilita la comprensione di quanto è possibile effettuare con il programma, ma non evidenzia le procedure che esso mette in atto. Interactive Physics, infatti, ricava le posizioni occupate dagli oggetti nella loro evoluzione temporale mediante il calcolo, secondo metodi numerici che consentono di trovare le soluzioni alle equazioni del moto anche in casi complessi, in cui analiticamente non è possibile procedere; il programma permette dunque di visualizzare il movimento di un oggetto sottoposto all'azione di forze, quali l'attrito o la resistenza dell'aria, che non sono costanti. Ciò che è rappresentato attraverso una modalità figurativo-analogica è la previsione del movimento ottenuta combinando leggi della dinamica e metodi di calcolo. Non a caso, l'ambiente è anche chiamato micromondo newtoniano.
Con IP il ruolo dell'utente è diverso da quello ricoperto operando con
Excel, in cui era necessario scrivere il modello con il linguaggio proprio del
programma. Il programma Interactive Physics richiede che nella produzione di
una simulazione l'utente inserisca dei valori che riguardano due aspetti: da
un lato devono essere esplicitate le caratteristiche del sistema che si desidera
rappresentare, sia quelle relative agli oggetti che costituiscono il sistema
sia quelle riguardanti le interazioni tra di essi o con l'ambiente (ad esempio,
è possibile escludere la forza gravitazionale). D'altro canto, in modo
non meno rilevante, è possibile ottenere rappresentazioni diverse dello
stesso sistema variando il metodo numerico utilizzato per risolvere l'equazione
di Newton (esiste più di un modo per ottenere i dati con il metodo dell'integrazione
numerica) o l'ampiezza dell'intervallo di integrazione.
Il programma non fornisce soltanto una rappresentazione analogica della situazione concreta. Nella simulazione realizzata con IP è possibile inserire degli "oggetti" che forniscono i valori di grandezze prescelte, vuoi in forma di grafico cartesiano vuoi numerica. Se la tipologia delle rappresentazioni è la stessa che viene utilizzata nell'esperimento reale, questo può tradursi nel vantaggio di favorire il confronto dei dati; tuttavia può anche provocare confusione tra misura oggettiva di grandezze fisiche e rappresentazione di un modello matematico descrittivo, comunque distinto dalla realtà.
Per rappresentare una situazione reale è stata realizzata la seguente simulazione (7), con il programma IP (sorgente IP):
Simulazione del movimento di una carrello lungo una guida a basso attrito; il carrello è stato dotato di "vele" di diverse dimensioni, per avere indicazioni sull'effetto della resistenza dell'aria sul moto.
La simulazione è stata costruita in modo da consentire di variare il
valore della forza con cui è spinto inizialmente il carrello. L'inserimento
di un grafico che rappresenti la velocità del carrello (8)
favorisce il confronto tra dati dell'esperimento reale e della simulazione (come
si può vedere nella simulazione
così modificata / sorgente IP).
E' possibile simulare l'ambiente in cui si trova il carrello secondo tre situazioni
differenti: privo di resistenza dell'aria, con resistenza bassa, con resistenza
alta. Queste condizioni forniscono comportamenti diversi per quanto riguarda
il movimento dell'oggetto (9). Se si confronta la situazione
simulata con l'esperimento reale si può stabilire quale comportamento
sia più rispondente alla situazione reale, e questa associazione comporta
una scelta anche per quanto riguarda la formulazione matematica della descrizione
del fenomeno.
Osserviamo uno dei grafici relativo all'esperimento reale:
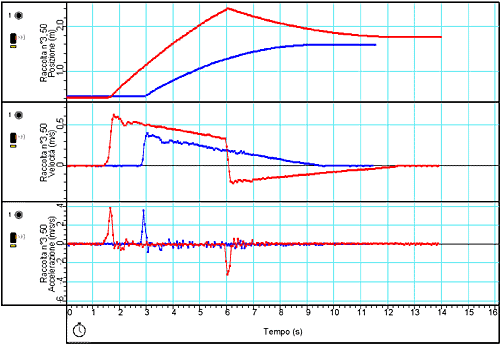
Queste due misure riguardano il moto di un carrello lungo la guida orizzontale, con due spinte iniziali diverse. La simulazione può rappresentare le due situazioni. Agendo sulla resistenza dell'aria si può decidere quale condizione si adatta maggiormente ai dati presi.
Se si riflette sull'origine della descrizione del fenomeno ottenuta attraverso il programma si potrà evidenziare come essa rappresenta le previsioni di evoluzione del sistema basate sulla formulazione del legame forza-accelerazione assunto da Newton: è quindi una descrizione del fenomeno in oggetto secondo la visione di Newton. Ciò che consente all'utente la rappresentazione è quindi la scelta di un modello descrittivo del fenomeno sulla base della dinamica newtoniana, modello che una volta individuato potrà produrre, se implementato, l'evoluzione del sistema sia in forma numerica (le tabelle con i dati ricavati risolvendo numericamente l'equazione) sia in forma grafica (l'andamento su un grafico cartesiano della posizione in funzione del tempo) sia in forma di animazione (il risultato di un processo che più che simulazione sembrerebbe corretto chiamare modellizzazione).
Se riflettiamo sul ruolo della simulazione sotto l'aspetto della conoscenza della fenomenologia, da quanto appena visto emerge come solo il confronto con la misura effettiva consente di individuare quale modello descrive adeguatamente il fenomeno, e ha quindi un valore determinante: senza di esso, tutte le possibili simulazioni che possono essere pensate hanno lo stesso valore.
La possibilità di confrontare modelli e realtà produce anche una conseguenza di carattere fondante: il fatto che si riesca a trovare una corrispondenza tra modello e fenomeno ci rassicura sulla validità della visione newtoniana del mondo.
Questi aspetti di valore non vengono adeguatamente esplicitati da una rappresentazione per immagini, quale quella fornita da IP, ma possono nascere dalla riflessione fatta sulle strutture linguistiche (anche se in linguaggio matematico), che rimangono quasi sempre ben nascoste quando viene utilizzato questo programma, soprattutto se si usa soltanto per mettere in azione l'animazione anziché per crearla; al contrario, le strutture linguistiche sono ben più chiare quando, per ottenere una simulazione di un fenomeno, si sviluppa un calcolo con dei risultati (come nell'esempio in cui gli allievi stessi hanno portato avanti l'evoluzione del modello elaborato a partire dai dati iniziali), come quando si utilizza il programma Excel per sviluppare lo stesso modello. Se questo può essere uno svantaggio della rappresentazione per immagini, è controbilanciato dal notevole vantaggio di essere decisamente più immediata ed esplicativa delle altre due rappresentazioni, quella tabulare e quella grafica. E' possibile non rinunciarvi: la comprensione delle strutture che la sorreggono e del ruolo che ha l'utente nel processo di realizzazione dell'animazione riesce ad attribuire un significato a tutto il processo.
Per valutare quanto è stata recepita in classe la sottounità si propone una domanda specifica che potrebbe essere inserita in una prova del tipo della "terza prova" dell'Esame di Stato
Essa potrebbe essere formulata così:
|
Si immagini di avere due grafici della velocità di un oggetto in funzione del tempo: il primo, (a), proveniente da una misura durante un esperimento, il secondo, (b), relativo ad una costruzione dello stesso esperimento tramite un software di modellizzazione. Essi risultano sovrapponibili. |
Nella risposta, per cui si dovrà prevedere un numero massimo di righe, dovrà comparire il fatto che (a) registra i valori effettivi della velocità mentre il fenomeno accade; in (b) sono tracciati i valori previsti per la velocità sulla base delle ipotesi inserite nella costruzione della rappresentazione del fenomeno e della meccanica di Newton. L'informazione fornita dai due grafici è differente, e il fatto che i due grafici siano sovrapponibili porta a pensare che le scelte operate nella costruzione del modello sono valide e che la meccanica newtoniana descrive in modo soddisfacente l'evoluzione del fenomeno reale.
L'esercizio proposto dalla sottounità del prof. Ragazzon può essere strumento di verifica sulla prima parte di questo percorso: si considera quindi valido tale esercizio anche per essa.
Il contenuto della sottounità ha avuto spunto dall'ampio e approfondito lavoro svolto riguardo ai temi di didattica della Fisica dall'Unità di Ricerca per la Didattica della Fisica dell'Università di Udine (URDUD), diretta dalla professoressa Marisa Michelini. Tra i numerosi temi specifici oggetto di ricerca c'è anche quello relativo alla modellizzazione. Il sito del Centro Interdipartimentale di Ricerca Didattica (CIRD) dell'Università di Udine riporta informazioni sulle diverse attività svolte e in corso.
(1) La metodologia prescelta è stata determinata dai vincoli di tempo per lo sviluppo del tema: una metodologia alternativa, forse più incisiva, prevederebbe lo svolgimento con la classe dell'esperienza di laboratorio e solo in seguito della parte qui riportata; tuttavia, sarebbe allora necessario poter usufruire di un laboratorio con apparato di acquisizione dati in linea con l'elaboratore del tipo di quello utilizzato nell'esperienza descritta, oltre che del software di modellizzazione Interactive Physics.
(2) Il programma Interactive Physics, software di modellizzazione che simula l'evoluzione secondo la Meccanica Newtoniana di sistemi fisici definiti dall'utente mediante una particolare interfaccia grafica, è prodotto dalla MSC Software. Informazioni sul programma (e una versione dimostrativa) possono essere reperite presso il distributore italiano dello stesso, all'indirizzo: http://www.campustore.it/. In particolare, una descrizione delle possibilità offerte dal programma è alla pagina http://www.campustore.it/ip; simulazioni già costruite, da poter scaricare, si possono trovare (oltre che in molti altri siti) alla pagina: http://www.campustore.it/ip/simulazioni_ip5.asp
(3) Il programma Science Workshop permette di raccogliere dati attraverso strumentazione in linea con l'elaboratore e di operare con essi. Il software è quindi parte del sistema completo di acquisizione dati, sviluppato dalla ditta Pasco scientific, ma può essere scaricato gratuitamente dal sito della ditta. Notizie su tutto il sistema possono essere trovate all'indirizzo http://www.elitalia.it, (o, più specificamente, all'indirizzo http://www.elitalia.it/online.html) della ditta ELItalia, escusivista italiano della Pasco scientific; anche da qui è possibile raggiungere il sito della casa madre, http://www.pasco.com.
(4) L'insegnante inserisce i dati nelle formule proposte e si ricava i valori scritti. Si può anche coprire in un primo tempo la tabella.
(5) NOTA PER L'INSEGNANTE: Nello spazio di 2 ore non è possibile eseguire effettivamente l'esperimento con i ragazzi; tuttavia, con un tempo a disposizione maggiore, sarebbe auspicabile portarlo a termine, sempre ammesso di avere l'attrezzatura necessaria.
(6) nella modalità edit, che permette di creare simulazioni e non soltanto di eseguire quelle già realizzate.
(7) Chi non potesse aprire le simulazioni con il programma IP può comunque avere un'idea del contenuto attraverso i video che le riproducono. In questo caso non è però possibile, purtroppo, interagire.
(8) per inserirlo, come si vede nel video registrato, dopo aver selezionato l'oggetto è sufficiente andare sulla voce di menù misura e scegliere velocità, nella componente x.
(9) Se si sta osservando la simulazione con IP si può andare alla voce di menù Sistema, quindi alla voce Resistenza dell'aria, modificare qui le condizioni e far ripartire l'animazione.