a. Situazioni problematiche relative ad alcuni connettivi e quantificatori.

Esempio1       Ali, Bili, Cili, Dili, Eli sono cinque alunni della vostra classe.       Ali, Bili, Cili        sono perfezionisti;       Ali, Cili, Dili        non sono conformisti;       Ali, Bili, Eli         sono indagatori Chi dei cinque alunni   è perfezionista e  indagatore ? Chi dei cinque è equilibrato o  è indagatore? Chi dei cinque  non è perfezionista, non è conformista e non è indagatore?         SPIEGA IL TUO RAGIONAMENTO

Esempi di soluzione dell'esercizio

a.

b.

 

 

Note per l'insegnante e osservazioni

• In classe si è stabilito che ogni volta che si incontra il connettivo  "o" lo si intende con valore inclusivo. Ciò per non creare ambiguità.

• Si ritiene di fondamentale importanza chiedere sempre agli alunni di motivare le loro scelte per evitare risposte casuali.

• Una parte della classe ha preferito lavorare utilizzando i diagrammi di Eulero-Venn, l'altra parte ha costruito una tabella (vedi esempi di soluzione).

 

Esempio2 Le cinque ragazze della stanza 119 sono uscite di nascosto per esplorare Londra. Si sa che: 2 hanno  portato con sé almeno i soldi e la carta topografica; 1 ha portato i soldi e la carta topografica; 3 hanno portato almeno la torcia; 3 hanno in tasca almeno i soldi; 1 ha solo la torcia; 1ha con sé il temperino e la torcia; 1 ha i soldi, la torcia e la carta topografica. Tra le cinque ragazze è possibile che qualcuna non abbia alcuno degli oggetti nominati? Quante potrebbero avere un solo oggetto? SPIEGA IL TUO RAGIONAMENTO

 

Esempio 3 Le 5 ragazze della stanza 119 contano i soldi per vedere se, raggiungendo Londra, potranno andare a mangiare una pizza. In tutto hanno 58 euro. Se Ambra avesse 3 euro in meno, Lucia 3 euro in più, Cristina 1/3 degli euro che ha Evelina la metà e Marta il doppio, allora avrebbero tutte  gli stessi soldi. Quanti euro ha ogni ragazza? SPIEGA IL RAGIONAMENTO

Esempio 4 Parlando di Londra e dei suoi abitanti ogni occupante della stanza fa una sua affermazione: - tutti i Londinesi sono Inglesi; - tutti gli Inglesi sono Europei; - alcuni Inglesi sono Londinesi;   - non tutti i Londinesi sono Protestanti; - non tutti i Protestanti sono Europei: Indica allora quali degli enunciati seguenti sono veri (V) e quali sono falsi (F). Tutti i Londinesi sono Protestanti    V    F Alcuni Inglesi sono Protestanti    V    F Alcuni Londinesi sono Inglesi    V    F Esiste almeno un Europeo che non è protestante    V    F SPIEGA IL TUO RAGIONAMENTO

Osservazioni

Esercizi di questo tipo sono stati dati più volte nel corso degli studi.
Generalmente l’alunno li risolve utilizzando i diagrammi di Eulero-Venn.    
Gli alunni dimostrano qualche difficoltà ad accettare che se l’universale è vera, anche l’esistenziale è vera.
Nel caso dell’ esercizio dato il maggior numero di errore si riscontra proprio nella terza risposta

b. Situazioni problematiche relative ad analogie strutturali tra connettivi logici e circuiti elettrici

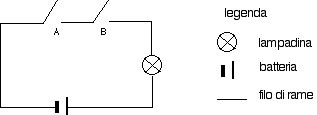
Esempio 1 Mentre stai cercando qualcosa per aprire la porta trovi il seguente schema: Perché la lampadina si accenda come devono essere i due interruttori? Rispondi dopo aver completato la tabella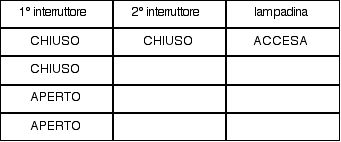 Ora considera l’ enunciato logico: Francesco ha i pantaloni bucati e la maglia rossa. Perché l’ enunciato sia vero, come devono essere i due enunciati semplici? Rispondi: Confrontando il circuito e l’enunciato al posto di cosa stanno gli interruttori? Il circuito chiuso o aperto a cosa corrisponde?e la lampadina accesa?

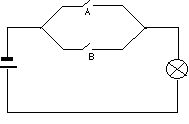
Esempio 2 Ragiona sul seguente schema: Perché la lampada si accenda come devono essere i due interruttori?  Rispondi motivando la tua scelta. Questo tipo di circuito ti ricorda un connettivo logico? Quale? MOTIVA LA TUA RISPOSTA.

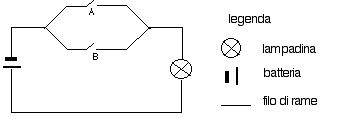
Esempio 3 Considera lo schema: SPIEGA LA TUA SCELTA.

Osservazioni

Gli alunni di terza media risolvono facilmente la prima parte dell’esercizio osservando lo schema.
Chi non ci riesce può lavorare con il circuito da loro stessi costruito.
Incontrano, invece, maggior difficoltà nel rispondere alla seconda domanda  perché il linguaggio logico - formale richiede buona capacità di astrazione che non tutti, a questa età, dimostrano di possedere.

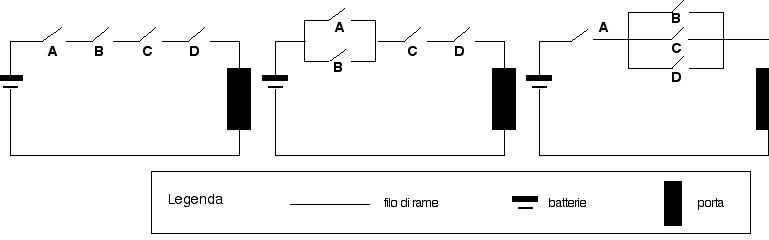
Esempio 4 Per aprire la porta della loro camera, che ha una chiusura di sicurezza, Ali,, Bili, Cili e Dili  hanno a disposizione una chiave ciascuno. Si sa che è indispensabile la chiave posseduta da Ali e almeno una delle altre tre chiavi. a. Quale dei circuiti in figura rappresenta la situazione? b. Su quale interruttore agisce la chiave di Ali?   c. È importante l'ordine in cui si usano le chiavi? Perché? d. Scrivi l'espressione logica corrispondente al circuito che rappresenta la situazione problematica.

Esempio 5 Per aprire la porta della stanza si hanno a disposizione tre chiavi: di queste, due sono indispensabili. Si sa che il circuito che la fa aprire ha al massimo cinque interruttori. Rappresentare la/le situazione/i indicando con A, B, C, ecc gli interruttori. Per ogni circuito disegnato indica le chiavi che non possono mancare. Scrivi le espressioni logiche corrispondenti ai diversi circuiti da te rappresentati.

Esempio 6 Per aprire la porta della stanza sono necessarie due delle quattro chiavi possedute dalle persone che la occupano, ma nessuna chiave è indispensabile. Quale circuito rappresenta la situazione? Disegnalo. Due persone hanno perso la loro chiave, ma fortunatamente è ancora possibile aprire la porta: su quali interruttori potrebbero agire le chiavi perse? In quali casi la porta non potrebbe venire aperta? Scrivi l'espressione logica corrispondente al circuito che rappresenta la situazione.