7. Descrizione delle fasi del lavoro
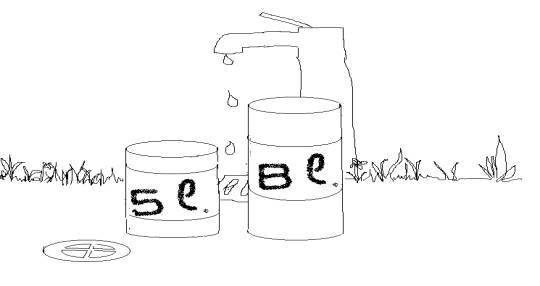
a) Alla classe viene proposto il seguente problema, corredato dal disegno:
Giorgio sta facendo degli esperimenti con l’acqua in giardino.
Ha a disposizione il rubinetto e due contenitori
di cui conosce la capacità:
il primo contiene 5 litri, il secondo 8 litri.
A Giorgio servono esattamente 2 litri d’acqua.
Come può fare per ottenerli? (scrivi
un elenco di tutte le manovre che dovrà fare)
Che manovre dovrà fare, invece, per ottenere
1 litro d’acqua?
N.B. Il problema può essere risolto
individualmente o a coppie.
 |
Questa seconda modalità di esecuzione favorisce la discussione ed una maggiore consapevolezza, quindi consente di proporre il problema ad alunni più giovani.
b)
L’insegnante si mette
a disposizione della classe per rispondere ad ogni quesito.
E’
importante ribadire che il materiale elencato è il solo che è
consentito utilizzare.
c)
Gli alunni si mettono all’opera
e ricercano i primi tentativi di soluzione, eventualmente utilizzando la
scheda allegata.
PRIMA SOLUZIONE: PER OTTENERE 2 LITRI
FASE OPERATIVA |
DEDUZIONI |
SITUAZIONE |
1 riempio il contenitore da 5 litri |
|
Il contenitore da 5 è pieno, quello da 8 è vuoto |
2 verso l’acqua nel contenitore da 8 litri |
So
che il contenitore da 8 litri può contenere ancora 3 litri
|
Il
contenitore da 5 è vuoto, quello da 8
è pieno fino a 5 litri
|
3 riempio nuovamente il contenitore da 5 litri |
|
Il contenitore da 5 è pieno, quello da 8 è pieno fino a 5 litri
|
4 verso l’acqua del contenitore da 5 litri in quello da 8 finchè questo ne può contenere |
Posso versare soltanto 3 litri, perciò nel contenitore da 5 restano i 2 litri che mi servono |
Il contenitore da 8 è pieno, quello da 5 contiene 2 litri .
|
SECONDA SOLUZIONE: PER OTTENERE 1 LITRO
FASE OPERATIVA |
DEDUZIONI |
SITUAZIONE
|
|
1 riempio il contenitore da 8 litri |
|
Il
contenitore da 8 litri è pieno, quello da 5 è vuoto
|
|
2
travaso l’acqua, riempiendo fino all’orlo
il contenitore da 5 litri |
Nel
contenitore da 8 mi sono rimasti 3 litri |
Il
contenitore da 5 è pieno, quello da 8 contiene 3 litri
|
|
3
vuoto il contenitore da 5 litri |
Posso
nuovamente utilizzare il contenitore da 5 litri |
Il
contenitore da 5 litri è vuoto, quello da 8 contiene 3 litri
|
|
4
verso i 3 litri nel contenitore da 5 litri |
Ora
so che il contenitore da 5 può contenere ancora 2 litri |
Il
contenitore da 8 è vuoto, quello da 5 contiene 3 litri
|
|
5
riempio nuovamente il contenitore da 8 litri |
|
Il
contenitore da 8 è pieno, quello da 5 contiene 3 litri
|
|
6
travaso nel contenitore da 5 litri tutta l’acqua
che può contenere |
Poiché
ho potuto versare soltanto 2 litri, ora nel contenitore da 8 litri
sono rimasti 6 litri |
Il
contenitore da 5 litri è pieno, quello da 8 contiene 6 litri
|
|
7
vuoto il contenitore da 5 litri |
Potrò utilizzarlo nuovamente |
Il
contenitore da 5 è vuoto, quello da 8 contiene 6 litri
|
|
8
con l’acqua rimasta nel contenitore da 8 litri
riempio il contenitore da 5 |
Nel contenitore da 8
litri resterà il litro che mi serve |
Il
contenitore da 5 litri è pieno, quello da 8 contiene 1 litro.
|
8.
Attività previste
Chiarificazione
della situazione problematica presentata da parte dell’insegnante.
Breve discussione collettiva
Gli alunni sono molto incuriositi dal problema ed intuiscono che la soluzione non è di tipo aritmetico.
Fanno molte domande all’insegnante cercando soluzioni pratiche che prevedono la modifica dei contenitori:
“Possiamo segnare con un pennarello (o un chiodo se il contenitore è di metallo) l’interno del contenitore?”
“Possiamo usare un altro contenitore graduato?”
“Possiamo misurare con una stecca l’interno dei barattoli e dividerlo in parti?” ...
L’insegnante chiarisce che queste proposte non sono accettabili e bisogna trovare la soluzione effettuando dei travasi.
Discussione
in coppia per facilitare la comprensione delle varie fasi del lavoro.
L’insegnante organizza gli alunni in coppie per facilitare la comprensione delle varie operazioni necessarie, l’elaborazione delle informazioni e la comunicazione.
Gli alunni si mettono al lavoro, immaginando e registrando graficamente
le fasi della soluzione.
PRIMA PARTE: PER OTTENERE 2 LITRI
Disegno
e descrizione delle varie fasi.
Per facilitare la riflessione, l’insegnante distribuisce una tabella di registrazione ad ognuna delle coppie.
Questo problema si presta più di altri ad una ricerca di soluzione per tentativi ed errori.
Per alcuni bambini può essere necessario suggerire l’operazione di avvio (parti dal contenitore da 5 litri).
Se l’insegnante pensa che questa prima fase
sia comunque troppo complessa per i suoi alunni, è possibile semplificare
il problema modificando il testo come segue:
Giorgio sta facendo degli esperimenti con l’acqua in giardino.
Ha a disposizione il rubinetto e due contenitori
di cui conosce la capacità:
il primo contiene 5 litri, il secondo 8 litri.
A Giorgio servono esattamente 3 litri
d’acqua.
Come può fare per ottenerli? (disegna
e descrivi le manovre che dovrà fare)
SECONDA PARTE: PER OTTENERE 1 LITRO
Nello svolgimento della seconda parte del problema gli alunni si avvalgono delle informazioni che hanno acquisito nella parte precedente. Alcuni però faticano a comprendere che è necessario partire riempiendo il contenitore da 8 litri (fissità funzionale).
Anche in questo caso risulta proficuo utilizzare la tabella per la registrazione dei dati e delle informazioni.
Questo problema, visto
il succedersi delle numerose manovre necessarie per la soluzione, si presta
in modo ottimale ad una riflessione sulla soluzione anche attraverso l’uso
di annotazioni simboliche e del diagramma di flusso.
9.
Strumenti previsti:
Materiale carta, penne, colori, eventuale scheda di registrazione
Attrezzature contenitori della misura data, acqua, vasca di scarico
Spazi classe, giardino.
10. Tempi necessari – scansione
temporale
Due ore per la soluzione teorica
Quattro ore per la soluzione concreta
11. Docenti coinvolti e dimensione
del gruppo degli alunni
Insegnanti di matematica con il gruppo classe
PER OTTENERE 2 LITRI
CHE COSA FACCIO |
CHE COSA SO |
DISEGNO |
|
|
|
|
Suddividi
la tabella elencando le diverse fasi.
PER OTTENERE 1 LITRO
CHE COSA FACCIO |
CHE COSA SO |
DISEGNO |
|
|
|
|
Suddividi
la tabella elencando le diverse fasi.























