1. SCELTA DELLE CARATTERISTICHE DEGLI EROI ED ABBINAMENTO EROE - ALUNNO
Tempo previsto:
- 2 ore
Obiettivi specifici:
- risolvere un problema utilizzando il diagramma ad albero
- saper costruire l'algoritmo che risolve una situazione problematica rappresentandola con un diagramma di flusso
Prerequisiti:
- conoscere il diagramma ad albero
- conoscere il diagramma di flusso
- saper risolvere semplici esercizi di combinatoria
Descrizione dell'attività
L'insegnante spiega agli alunni che ogni eroe dovrà possedere o non possedere alcune caratteristiche, che verranno espresse mediante criteri oggettivi al fine di classificare gli eroi - alunni.
L'insegnante pone alla classe il seguente problema:
Quante caratteristiche sono necessarie affinchè, in una classe, composta di 18 alunni, ogni alunno vesta i panni di un "eroe" diverso da tutti gli altri per almeno una caratteristica?
Gli alunni dovranno risolvere il problema lavorando a coppie.
Questo tipo di problema è stato assegnato in una classe a coppie di ragazzi, e i risultati emersi dall’esperienza sono stati i seguenti: solo una coppia ha cercato di risolvere il problema senza seguire una procedura ordinata e non è arrivata alla soluzione, tutte le altre hanno utilizzato procedure ordinate.
Riportiamo qualche esempio di soluzione:
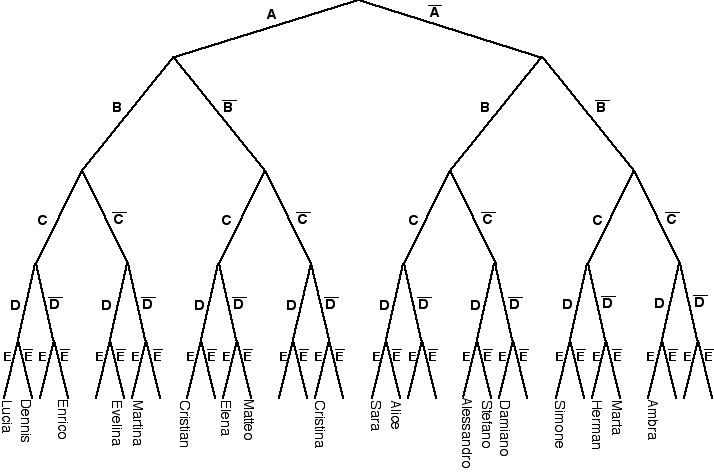
Una coppia di alunni ha costruito il diagramma ad albero completo.
Dal confronto dei lavori svolti e dalla discussione, gli alunni hanno constatato che:
- procedure ordinate permettono di ottenere più facilmente risultati corretti;
- riconoscere le analogie con problemi già svolti facilita la soluzione;
- individuare che c'è qualcosa che si ripete sempre uguale abbrevia il lavoro;
- individuare relazioni tra i dati permette di risolvere il problema anche senza la rappresentazione grafica.
A questo punto l'insegnante presenta cinque qualità degne dell'eroe, qualità qui indicate con lettere maiuscole:
A, B, C, D, E
(le qualità variano a seconda del tipo di scenario scelto: più avanti verrà fornito un esempio concreto su uno scenario scelto da noi)
Una volta che sono state individuate le cinque caratteristiche l'insegnante chiede a ciascun alunno di costruire un diagramma ad albero che rappresenti tutti i casi possibili. Ogni cammino dell'albero corrisponde ad un possibile, unico "eroe". Tuttavia i cammini sono 32 e gli alunni 18; si decide quindi di assegnare casualmente ad ogni allievo un cammino, fatta eccezione per quello caratterizzato da assenza di caratteristiche in quanto l'eroe, vista la natura del gioco, non potrebbe partecipare. Per far ciò l'insegnante dovrà aver già predisposto un elenco degli alunni in più copie e 31 bigliettini su ciascuno dei quali c' è scritto un numero da 1 a 31.
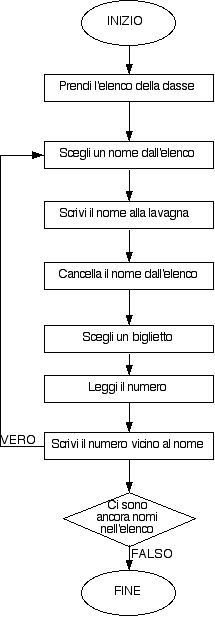
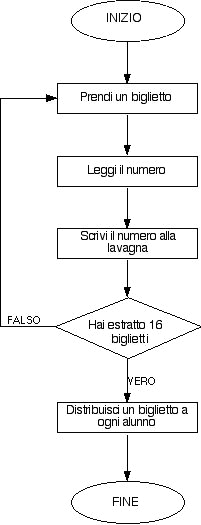
Gli allievi, lavorando in coppia, dovranno scrivere, in forma di algoritmo, una procedura per determinare a quale cammino - ognuno di loro risulti abbinato.
Riportiamo, come esempio, le procedure scelte che ci sembrano più significative.
|
|