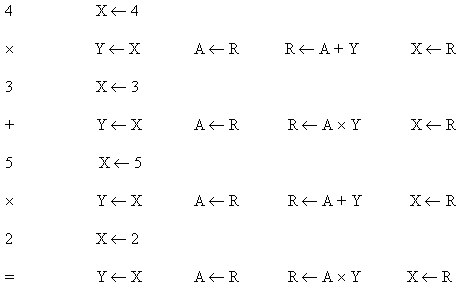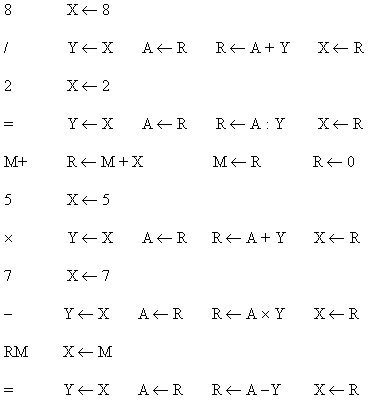L'Informazione entra in Macchina   L'ELABORAZIONE DEI DATI

Da sempre l’uomo ha cercato di dotarsi di mezzi che aumentino le sue capacità manuali e la sua forza inventando macchine che possano lavorare al suo posto. Oggi, liberato dalla fatica fisica, egli si concentra su un compito più nobile: il comando ed il controllo di macchine che elaborino informazioni.Come comunica con esse? Quali le aspettative e quali i limiti? Nell’era digitale in cui sembra che ogni problema possa essere risolto dall’elettronica, analizzare il percorso dell’informazione, le modalità della sua elaborazione ed i suoi possibili effetti è la base da cui partire per avvicinarsi alle macchine con spirito critico per cercare di sfruttare in modo ottimale le opportunità offerte dalle nuove tecnologie.

• Rilevare che qualsiasi macchina è cablata e di conseguenza ci sono dei limiti fisici alle richieste
• Rendere consapevoli che la potenza dei computer è comunque il risultato della logica e della tecnologia prodotte dal genio dell’uomo e che quindi dietro alla “magia” di ogni macchina elettronica c’è un progetto umano con tutti i limiti che tale umanità comporta
• Ridimensionare il sogno del robot tutto-fare e tutto-pensare

• Capire come si può automatizzare il calcolo binario
• Seguire il percorso dell’informazione
• Trovare l’algoritmo di valutazione di una espressione numerica
• Ragionare su potenzialità e limiti della rappresentazione dei numeri
• Potenziare il concetto di precedenza delle operazioni nelle espressione numeriche
• Motivare un uso numerico dei prodotti notevoli
• Rivalutare il ruolo dello studio dell’hardware nell’analisi delle potenzialità ma anche dei limiti delle macchine elettroniche

Alla fine di ogni singola lezione si possono trovare esempi di esercizi, schede esplicative per gli alunni, complementi per gli insegnanti.
Gli oggetti usati nel corso delle lezioni sono invece presentati e illustrati nell’appendice.
In relazione a questo modulo è disponibile l’applicazione interattiva PocketCalculator, accessibile attraverso le pagine ipertestuali di questa unità. Tale strumento offre una visione della dinamica interna di una calcolatrice elementare e premette di visualizzare possibili percorsi dei dati.

1. ricordare le sequenze delle operazioni da svolgere,
2. ricordare gli algoritmi necessari ad eseguire le singole operazioni,
3. ricordare i numeri che intervengono in tali operazioni.

• si fa “girare” il programma relativo all’operazione scelta girando la manovella,
• il risultato viene registrato in una fila di finestrelle.

La registrazione su di esse di un risultato intermedio evita di doverlo ricordare a memoria o trascrivere su un altro supporto, come avveniva nell’abaco; è per questo che potremmo chiamare questa fila di finestrelle “registro di memoria”. Nei dispositivi elettronici tale funzione è svolta da una serie di elementi binari, detti flip-flop, che sono i componenti elementari della memoria.

Osserviamo ora una calcolatrice elementare.
Facendo riferimento alla struttura generale di una “macchina elettrica” introdotta nel modulo precedente, possiamo dire che una calcolatrice

• “sente” attraverso la pressione dei tasti,
• “agisce” mostrando i risultati sul visore.

Ne abbiamo progettato il codificatore: l’interfaccia di input. Un analogo decodificatore costituisce l’interfaccia di output.
Ora sappiamo che si può disporre di un dispositivo adatto alla registrazione-conservazione di un carattere numerico e che ogni numero viene quindi memorizzato attraverso una serie di flip-flop che formano un registro. La codifica per tale registrazione è ovviamente di tipo binario.

Le reti con retroazione che realizzano alcuni flip-flop (flipflop_nor, flipflop_nand, flipflop_rs) sono incluse tra i progetti già predisposti per essere utilizzati con il programma di simulazione delle reti logiche e possono essere selezionati direttamente dal menù.

Esercizi proposti

ripasso della numerazione in base 2 e BCD con le relative trasformazioni



Note per l’insegnante

• Se schematizzare un rudimentale codificatore è stato abbastanza agevole, è difficile far comprendere il funzionamento di un flip-flop al livello scolare proposto per questa unità. Sarà sufficiente darne una definizione elementare.
  

• Per il registro potrebbe risultare utile anche l’analogia con una striscia di nastro per registratore suddiviso in piccoli settori da un bit. Questa metafora può essere utilizzata specialmente quando, in fase di assegnazione, si deve sostituire un dato con un altro.
  

• Un’immagine elementare di flip-flop si può proporre osservando che un qualsiasi interruttore è, a tutti gli effetti, un flip-flop meccanico che memorizza “dove” è stata esercitata la pressione del dito l’ultima volta e mantiene la sua posizione fino all’arrivo della prossima pressione (dato).

 

Complementi

 

Seconda lezione

Il percorso dei dati

 

Per una migliore fruizione della presente lezione sarebbe opportuno che gli allievi disponessero di un numero adeguato di calcolatrici elementari. Con tale termine si intendono calcolatrici non scientifiche, né tanto meno programmabili, ma quelle la cui tastiera presenta i tasti numerici, quelli per una memoria (M+, M-, RM, CM) e poco altro (presumibilmente la radice quadrata e la percentuale). Nella simulazione che è stata preparata non compare il tasto M- ma è stato invece previsto il tasto di cambia segno che generalmente non si trova su tali calcolatrici. La motivazione di tale scelta verrà data nel seguito.

Lezione frontale
Attraverso un lucido o una calcolatrice aperta possiamo iniziare ad esaminare più da vicino la parte hardware di una calcolatrice. Si individuano l’unità di input costituita dalla tastiera, quella di ouput costituita dal visore ed una, ancora misteriosa, parte interna. Esse ricalcano la struttura già vista.

 

Sente		Decide		Agisce

Si è già visto come le interfacce trasformino i dati.
Attraverso il seguente schema generale vediamo ora come è organizzata la parte che “decide”. Come si può ben immaginare questa parte è composta da vari sottoinsiemi cablati. Noi non li osserveremo più dal punto di vista elettrico ma da quello della loro specifica funzione e per fare ciò esamineremo il percorso seguito dai dati durante l’esecuzione di un semplice calcolo.
Va sottolineato che in commercio vi sono numerosi tipi di calcolatrici ed ognuna di esse ha caratteristiche leggermente diverse sia nelle prestazioni offerte sia in alcune modalità di elaborazione per cui sequenze di digitazione di tasti uguali portano spesso a risultati diversi.
Nell’impossibilità di sceglierne una specifica, si è deciso presentare la simulazione di una calcolatrice nella quale le caratteristiche di elaborazione più comuni alle calcolatrici di base vengono illustrate nel loro percorso interno.

Questa simulazione intende raggiungere vari obiettivi:

• introdurre in modo semplice le componenti principali di una CPU,
• seguire le varie fasi di una possibile elaborazione dei dati,
• introdurre analogie con la corrispondente CPU di un computer,
• abituare gli alunni ad usare in modo consapevole una qualsiasi calcolatrice,
• fornire alcune basi per l’avvio all’uso dei linguaggi di programmazione.

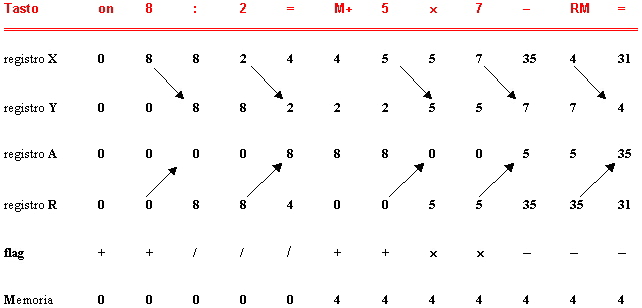
A tal fine viene proposto un semplice calcolo (per es. 12+5). Viene illustrato passo-passo il possibile comportamento delle componenti interessate (vedi complementi), senza fare riferimento a nessuna calcolatrice specifica. La procedura viene man mano seguita sulla simulazione o su lucidi appositamente preparati. (Dopo aver caricato la applet dal browser Internet Explorer, conviene premere il tasto-funzione F11 per vedere la simulazione a pieno schermo.)

Lavoro di gruppo

Prove di simulazione.

Esercizi proposti

Ricostruisci il percorso dei dati all’interno della tua calcolatrice e prepara lo schema corrispondente.

Esercizi di ripasso delle operazioni di addizione e sottrazione con numeri in base 2.

Note per l’insegnante

• Per usare correttamente la applet di simulazione si deve disporre di un browser e, per usufruire dello schermo intero, premere il tasto-funzione F11.
  

• L’insieme numerico utilizzato nella simulazione è quello dei numeri interi da –2048 a +2047.
  

• Pur disponendo della simulazione, conviene dare una prima spiegazione attraverso dei lucidi sulla lavagna luminosa o proiettare la simulazione stessa. Infatti la novità del “gioco” tende a distrarre gli allievi che non seguono la spiegazione ma cominciano a fare vari tentativi.
  

• Questa strategia dei tentativi è stata ipotizzata e potrebbe costituire un buon metodo di deduzione sulle procedure delle macchine ma è una attività la cui riuscita dipende molto dalla composizione della classe e dal suo comportamento a livello disciplinare.
  

• Dopo aver commentato adeguatamente il percorso è bene permettere agli allievi di sperimentare varie e numerose situazioni di calcolo.
  

• Il controllo del percorso da parte degli allievi crea una certa animazione nella classe anche perché non sempre con le calcolatrici a loro disposizione ottengono gli stessi risultati a parità di tasti premuti. A seconda della casa produttrice infatti le singole calcolatrici possono presentare comportamenti diversi. In particolare, alla fine dell’ultima esecuzione, nel registro Y potrà rimanere memorizzato l’ultimo dato, il primo o, per evitare gli errori da tasto ripetuto, lo zero.
  Tali comportamenti si evincono appunto premendo ripetutamente il tasto = .
  

• Nella calcolatrice che viene simulata nella lezione seguente si è scelto di mantenere la memorizzazione del secondo operando.

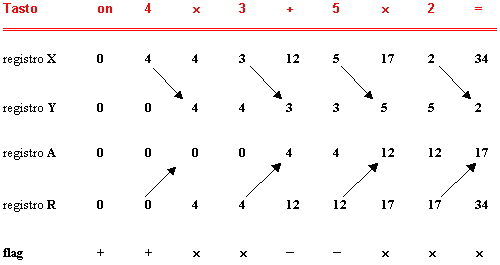
In previsione dell’uso di un linguaggio di programmazione si potrà riassumere la tabella nella seguente sequenza di assegnazioni, dove nella prima colonna compare il tasto premuto:

Laboratorio di computer

simulazioni

Esercizi proposti

tabelle di calcolo

Note per l’insegnante

• Gli esercizi proposti sono stati selezionati in modo da consentire il calcolo senza dover annotare dei numeri a parte.
  

• L’esercizio di riscrittura è risultato alquanto utile per rafforzare il concetto di precedenza delle operazioni e per sottolineare l’importanza di un uso corretto delle parentesi.
  

• Anche la proprietà commutativa, spesso appresa con annoiata rassegnazione, acquista in questo contesto una notevole e divertente rilevanza.
  

• Gli esercizi basati sulla assegnazione ai registri sono risultati un ottimo prerequisito alla programmazione.

Lezione frontale
Gli esercizi proposti per casa non richiedevano, se svolti correttamente, di ricordare a mente o di annotare su un foglio qualche risultato intermedio.

Come eseguire invece 5 x 7 - 8 : 2 ?

La necessità di conservare almeno un risultato parziale ha portato all’introduzione di un registro di memoria. Esso, come gli altri registri, contiene lo zero al momento dell’accensione ed il suo contenuto nelle calcolatrici più comuni, viene modificato dai seguenti tasti:

• M+ annota nel registro di memoria la somma di quanto già vi era contenuto con il numero presente nel registro X
• M- annota nel registro di memoria la differenza fra quanto già vi era contenuto e il numero
  presente nel registro X
• RM copia in X il contenuto del registro di memoria
• CM azzera il registro di memoria

Nella simulazione il tasto M- è stato eliminato e sostituito con il tasto cambiasegno +. Tale scelta è stata motivata dalle seguenti considerazioni:

• l’algoritmo risolutivo di una sottrazione usa la somma algebrica tra il minuendo e l’opposto del sottraendo
• questo tipo di procedura offre la possibilità di parlare della rappresentazione binaria dei numeri negativi e dell’uso del complemento a due
• nel calcolo delle espressioni l’uso del cambiasegno offre una interessante possibilità di aggirare il problema della precedenza di una operazione non commutativa come la sottrazione e può suggerire la possibilità di sostituire una divisione con il prodotto del primo fattore con l’inverso del secondo.

La tabella corrispondente all’espressione precedente sarà la seguente:

con la relativa sequenza di assegnazioni:

Esercizi proposti

espressioni numeriche con uso della memoria

Note per l’insegnante

• La scelta di usare nella simulazione solo numeri interi può sembrare eccessivamente restrittiva ma, utilizzata con numeri non esattamente divisibili, può servire per portare gradualmente il discorso sulle approssimazioni e sulla affidabilità dei calcoli.
  

• Anche l’uso del cambiasegno serve a sottolineare come in Z quella che appare come una differenza sia in effetti una somma algebrica nella quale in segno – non è un operatore ma il segno del secondo addendo, per cui 5–7= –7+5. Ma anche 5–3x5 = –3x5+5 e quindi questo tipo di espressione si può eseguire senza l’uso della memoria.

Nell’ambito della matematica tradizionale, tutti i problemi ed esercizi usano numeri “corti”, con poche cifre decimali ma, specialmente nelle materie sperimentali, quando i calcoli vengono demandati ad uno strumento, sono da tenere in considerazione anche l’approssimazione, l’errore e la complessità del calcolo. La seguente lezione presuppone la conoscenza del sistema di rappresentazione dei numeri decimali anche in formato scientifico e dei concetti di arrotondamento e troncamento.

Intervista guidata
Durante la simulazione nel laboratorio i numeri coinvolti erano interi ed una eventuale divisione fra di essi dava come risultato la parte intera del quoziente ma, nello svolgere le espressioni assegnate per casa, anche partendo da numeri interi si sono ottenuti risultati decimali. Quanto sono attendibili? Tutti hanno ottenuto lo stesso risultato? Emergono differenze anche notevoli. Quale sarà la causa? Usando alcuni esempi si notano arrotondamenti e troncamenti. Basta questa differenza a giustificare le differenze tra i risultati?

Lavoro di gruppo
Viene consegnata una scheda con proposte di calcolo in modo da confrontare i risultati ottenuti attraverso differenti calcolatrici.

Lezione frontale
Limiti dei registri. Il calcolo approssimato.Se la classe è sperimentale PNI viene illustrata la configurazione in virgola mobile.


Note per l’insegnante

• Nelle calcolatrici non scientifiche la situazione di overflow fa sì che sul display compaia il numero seguito da una piccola E (per es. il risultato 9876543212 verrà espresso come 98.765432E corrispondente a 9876543200). Ciò impedisce il proseguimento di qualunque calcolo.
  

• I limiti dalla capacità dei registri della calcolatrice usata dagli alunni può offrire uno spunto per l’uso dei prodotti notevoli. Per esempio per ottenere il risultato esatto di 98761,7² difficilmente si otterranno i valori esatti dei quadrati ma si può aggirare l’ostacolo calcolando il prodotto equivalente (98760 + 1,7)² ed eseguendo parte del calcolo a mano. Analogamente per trovare il prodotto esatto fra due numeri, si può utilizzare la proprietà distributiva. La scelta di usare queste strategie dipende naturalmente dal numero di cifre visualizzabili sul display e dall’ordine di grandezza dei numeri. È questa una delle poche occasioni, specialmente per gli alunni dei licei, di riflettere sugli ordini di grandezza e sulla propagazione degli errori.
  

• Spesso nell’insegnamento della matematica si privilegia il calcolo letterale e raramente si affrontano problemi della vita reale. Ne deriva una conoscenza superficiale delle problematiche relative al calcolo numerico che sono comunque interessanti. A volte alcune cifre decimali sembrano alquanto trascurabili. Il seguente esempio può motivare la ricerca di una particolare precisione nel calcolo: un cubo di lato 873 mm viene rivestito di uno strato d’oro di 0,1 mm di spessore. Calcolare la quantità di oro usata.
  Lo spigolo ora misura 873,2 mm. Il volume del materiale usato si ottiene da
  
  
  
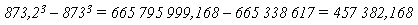
  dove è interessante notare l’ordine di grandezza dell’incremento generato dalla variazione di
  0,2 unità.
  

• Si può parlare di densità nell’insieme numerico della calcolatrice? Benché all’interno di linguaggi riferiti ai computer questi numeri vengano chiamati “real” la loro distribuzione sulla retta reale non è uniforma e il loro insieme non è denso. Spesso gli alunni non si rendono conto che una unità di differenza, quando il valore è espresso in formato scientifico, corrisponde ad una differenza reale dell’ordine di grandezza del valore stesso.
  

• Visto che la presente unità è rivolta ad alunni del primo anno del biennio non è possibile parlare di numeri reali ma si può ugualmente utilizzare i numeri decimali illimitati, ben conosciuti alle medie, per sottolineare come, nell’eseguire una espressione, il calcolo frazionario sia la soluzione ottimale per ottenere il massimo della precisione, come lo sarà nella seconda classe il calcolo con i radicali.

Lavoro di gruppo
Riallacciandosi alla prima lezione di questo modulo si può osservare che a questo punto abbiamo finalmente ottenuto uno strumento che ci solleva dall’impegno di memorizzare i numeri e le procedure per le operazioni elementari. Per risolvere un problema rimane però ancora la necessità di ricordare la sequenza di operazioni da svolgere per eseguire l’algoritmo. Vengono a questo punto proposti alcuni algoritmi di tipo iterattivo. I ragazzi vengono divisi a gruppi di tre. La sequenza dei tasti da premere viene “dettata” da uno di essi al compagno che sta usando la simulazione al computer o la propria calcolatrice. È una cosa noiosa e spesso ci sono fraintendimenti e si deve ricominciare da capo. Si conviene che servirebbe un esecutore preciso e paziente a cui dare delle precise indicazioni che possa leggere ed eseguire da solo. Quindi ogni gruppo cerca di accordarsi su una modalità di codifica. A seconda della modalità scelta (grafica o verbale) si possono formare gruppi più numerosi che elaborino un linguaggio comune.

Esercizi proposti

algoritmi

Note per l’insegnante

• Questo tipo di proposta, data la sua valenza formativa, richiederà almeno due ore se rivolta a classi sperimentali.
  

• Il curricolo prosegue ora su due vie:
  

• per gli allievi dei corsi tradizionali si continua con l’osservazione dele approssimazione e degli errori nelle materie scientifiche
  
  
• per gli allievi che seguono il corso di Informatica:
  
  
  • si approfondiscono le affinità con la struttura del computer,
  • si inizia a presentare il linguaggio prescelto,
  • si utilizza il concetto di assegnazione.