UD3

IL CONFINE TRA ANALOGICO E DIGITALE E LE UNITÀ DI MISURA INFORMATICHE

 

Se tutti i fenomeni vengono trattati come numeri, allora cadono le barriere tra suoni, immagini, testi e parole.

La comunicazione è solo bit, e tutto si mescola in un solo medium.

 

Prerequisiti

 

Contenuti

 

Obiettivi

 

 

Si fornisce agli/alle allieve una sintetica scheda sul sistema binario, che viene poi spiegata dall’insegnante.

Per verificare la comprensione del sistema binario e/o rafforzarla, dopo aver esaminato e discusso la scheda Far di conto nel sistema binario, si propongono agli/alle allievi/e alcuni esercizi.

 

 

Esempi di esercizi:

 

  1. Se vogliamo scrivere la parola Mamma in binario dobbiamo associare ad ogni lettera un numero binario, ad esempio M = 00, m = 01, a = 10; la parola corrisponderà alla stringa binaria : 0010010110. Inventa un codice binario per le lettere P, p, i, o e scrivi la parola Pippo utilizzando tale codifica.
  2. Inventa un codice binario per il tuo nome. Attento/attenta ogni lettera maiuscola deve avere un codice diverso dalla corrispondente lettera minuscola

 

 

Dopo aver affrontato le basi del sistema binario, si passa quindi ad esaminare il significato dei termini analogico e digitale, richiamando alla memoria gli strumenti di misurazione già presentati nell’UD1.

 

Si spiega che i termini si riferiscono a due diversi modi di rappresentare la parte quantitativa di una informazione.

Un grandezza analogica è proporzionale al valore che rappresenta.

Per la comprensione si porta ad esempio il termometro a mercurio.

Il mercurio di un termometro analogico sale e si abbassa di livello nella colonnina per indicare un aumento o diminuzione di temperatura.

Strumenti analogici sono anche il “barometro degli antichi” che essi/esse stesse hanno costruito e il dinamometro (l’allungamento della molla è proporzionale al peso).

Con il termine digitale si intende invece una grandezza identificata da un numero.

Si mostra un termometro digitale che visualizza direttamente il numero che indica il valore della temperatura momento per momento.

Ugualmente per l’orologio analogico e digitale. In entrambi i casi avviene la rappresentazione fisica dello scorrere del tempo.

Si chiede agli/alle allievi/e di descrivere il loro funzionamento.

Se il concetto è chiaro diranno che nel primo le lancette si muovono lungo il quadrante in maniera proporzionale al tempo trascorso. La loro posizione fisica descrive per analogia un altro fenomeno: il tempo.

La rappresentazione digitale fa invece un campionamento del fenomeno che rappresenta, non considera tutti i valori in una scala continua, ma li traduce in numeri con una determinata precisione.

La rappresentazione analogica riproduce invece con continuità il fenomeno .

 

Si propone a questo punto come esercizio: disegnare il grafico di un segnale analogico e quello di un segnale digitale.

 

 

A questo punto si descrivono sinteticamente I COMPUTER (non è compito del corso di scienze della materia approfondire l’argomento).

 

Si inizia dicendo che i computer lavorano utilizzando segnali elettrici (segnali analogici): per farlo devono essere dotati di una gran moltitudine di interruttori, che combinati insieme permettano di realizzare tutte le manipolazioni della “logica binaria”.

Si ricorda che la scelta del digitale per i computer (esistono anche computer analogici), in particolare per la forma basata su due stati soltanto (aperto/chiuso, acceso/spento,on/off, 0/1, sistema digitale binario), fu resa conveniente con l’imporsi del transistor.

Si continua dicendo che visto dal di dentro un computer non fa altro che aggregare e disaggregare combinazioni di simboli. Questi simboli sono 0, 1. Sono bit.

I bit hanno la forma di segnali elettrici che viaggiano dentro il computer e assumono due valori di tensione , 0 volt e 5 volt. Lo 0 volt rappresenta lo spento, il segnale 5 volt rappresenta l’acceso, il numero binario 1.

L’aver adottato nei computer un sistema di codici binario è utile perché corrisponde alla logica a due stati dell’hardware. A due stati è però anche la logica formale.

Ad ogni proposizione logica, infatti, si può associare un valore di verità, vero o falso.

Si chiede agli/alle allievi/e di formulare due proposizioni a cui attribuire un valore di verità.

Il criterio di verità non interessa, è esterno.

Quello che importa è l’associazione tra una frase e un valore.

Le proposizioni si possono combinare tra loro in vari modi , sì da ottenere come risultato sempre un valore vero o falso secondo il principio filosofico del terzo escluso.

Nei computer si stabilisce un molteplice livello di rappresentazione.

A livello elettrico si ha a che fare con segnali elettrici (0 volt e 5 volt)

A livello numerico con un mondo di numeri composto solo da 0 e 1, a livello logico con i valori vero o falso.

Nelle proposizioni logiche si possono eseguire operazioni per combinarle assieme.

 

Per far comprendere a studenti e studentesse del biennio delle superiori le proposizioni logiche e le più semplici operazioni e quindi le modalità di funzionamento di un computer, si fa ricorso alla costruzione di semplici circuiti elettrici .

 

Le più note e semplici operazioni logiche sono OR logico e AND logico.

 

Si chiede agli/alle studenti/studentesse di costruire con materiale semplice i circuiti elettrici sotto disegnati, dopo aver brevemente introdotto il concetto di circuito elettrico e descritto i suoi componenti.

L’obiettivo non è un’unità didattica sulla corrente elettrica e le sue leggi ma costruirsi uno strumento per comprendere la logica di un computer.

La costruzione dei circuiti viene assegnata come compito a casa. Le istruzioni per la costruzione si trovano sul libro di testo.




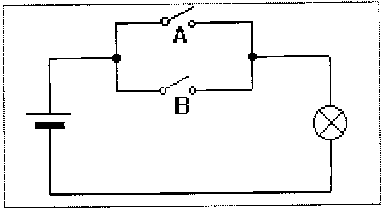
Circuito equivalente all’OR logico




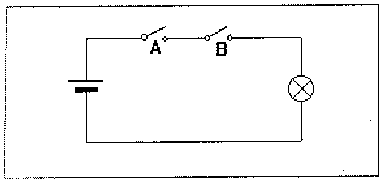
Circuito equivalente all’AND Logico

 


In classe viene analizzato l’OR LOGICO e l’AND LOGICO

 

ANALISI DI OR LOGICO

 

Questa operazione logica può essere rappresentata con un semplice circuito elettrico , composto da una batteria , da due interruttori e da una lampadina.

 

Gli allievi e le allieve riusciranno a capire aprendo e chiudendo gli interruttori qual è la verità dell’OR.

La verità dell’OR è rappresentata dall’accensione della lampadina, che avviene se l’interruttore A è chiuso o se l’interruttore B è chiuso e se lo sono tutti e due.

 

 

ANALISI AND LOGICO

 

Anche questa operazione può essere rappresentata da un circuito elettrico, composto da una batteria, due interruttori, una lampadina.

La verità dell’AND , come è facile verificare da parte degli allievi/e,è rappresentata dall’accensione della lampadina, che avviene se l’interruttore A è chiuso; diversamente la corrente non trova strada fino alla lampadina.

 

Prima di giungere a delle conclusioni si chiede quindi agli studenti e alle studentesse di compilare la tabella di verità dell’OR logico e la tabella di verità dell’AND logico.

 

 

Tabella di verità OR logico

A

B

A OR B

0

0

 

0

1

 

1

0

 

1

1

 

 

 

Tabella di verità AND logico

A

B

A AND B

0

0

 

0

1

 

1

0

 

1

1

 

 

A conclusione si potrà finalmente dire che naturalmente nei microprocessori non ci sono lampadine, ma che il principio è questo.

Usando operatori elementari del genere l’unità centrale dei computer trasforma le sequenze di bit in ingresso seguendo le istruzioni che le vengono dai programmi.

Gli operatori logici vengono realizzati con dei circuiti elettrici a transistor incisi direttamente nel silicio dei chips.

Muovendo e trasformando gli 0 e gli 1 dei bit si rappresentano di volta in volta realtà assai diverse: caratteri, colori, suoni, lettere.

 

 

 

Per completare la comprensione del significato dei termini analogico e digitale in relazione ai contesti in cui si applicano e per rispondere alle domande che spesso studenti e studentesse si pongono sul significato di memoria di un computer, si presentano alcune semplici esperienze sul magnetismo ed elettromagnetismo.

Come per i circuiti elettrici la trattazione dell’argomento magnetismo e elettromagnetismo è di tipo descrittivo; non si vuole effettuare uno studio quantitativo delle proprietà magnetiche ma solo far comprendere che la struttura fisica dell’informazione si basa sulla natura dell’elettromagnetismo.

 

Si mostra agli/alle studenti/studentesse una piccola lavagna magnetica e si chiede loro come attaccare un foglietto di carta alla lavagna magnetica.

Sicuramente alcuni/alcune risponderanno che è necessaria una piccola calamita.

Tutti/e hanno avuto occasione di avere tra le mani una calamita, ma pochi/e si sono chiesti di che cosa siano fatte e del perché aderiscono a lamiere di ferro e non a superfici di legno o di alluminio.

Si inizia quindi osservando che un magnete, qualunque sia la sua forma, presenta sempre due zone in cui la proprietà di attrarre si manifesta più intensa che altrove. Si introduce il concetto di poli magnetici, che si possono individuare disponendo attorno al magnete della limatura di ferro. La limatura di ferro mette in evidenza la posizione dei poli. Ai due poli si assegneranno i valori + e -.




 

 


Si propone agli/alle allievi/allieve di separare due magneti uniti a formarne uno e di ripetere l’esperienza con la limatura di ferro.

Ancora una volta si potrà verificare che i due poli del magnete non si separano, ma che si otterranno due nuovi piccoli magneti che hanno ancora due poli opposti.

 

Si chiede quindi agli studenti e alle studentesse se, a partire dalla loro esperienza, ritengono vi sia o possa essere una relazione tra magnetismo ed elettricità.

Per rispondere alla domanda o per verificare la correttezza delle risposte date, tutti/tutte insieme, si fa l’esperienza della visibilità del campo magnetico creato da un campo elettrico.

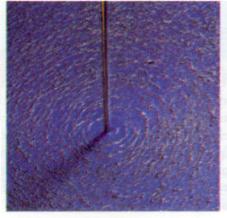
Su di un cartoncino attraversato perpendicolarmente da un filo conduttore si stende della limatura di ferro (foto1)

Si fa percorrere lungo il filo conduttore corrente elettrica e si chiede agli/alle allievi/e di descrivere il risultato e se possibile di trarre delle conclusioni.

Facilmente i/le ragazzi/ragazze diranno che la limatura di ferro si è disposta sul filo in cerchi concentrici con centro nel punto in cui passa il filo.

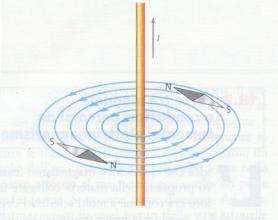
Per consentire agli/alle allievi/e di giustificare l’orientamento assunto dalla limatura di ferro con la presenza di un campo magnetico si dispone sul foglio un ago magnetico. Tutti/e osserveranno che esso si dispone lungo una direzione perpendicolare al filo e tangente alla circonferenza che passa per il centro dell’ago. (disegno 1)

Foto 1

Disegno 1

 

 

 

La conclusione a cui si giungerà è dunque che una corrente elettrica che attraversa un cavo metallico genera un campo magnetico. Questo campo magnetico è lo stesso che rende oggetti metallici permanentemente magnetizzati.

In una barra magnetica, il campo magnetico si estende dal polo nord al polo sud. In un cavo, il campo magnetico si forma intorno al cavo stesso. 

Stabilita l’esistenza di uno stato elettromagnetico della materia, si proseguirà dicendo che in certe sostanze lo stato elettromagnetico può essere facilmente alterato e che una volta stabilito

viene conservato inalterato finché non viene nuovamente mutato da una forza esterna.

 

Si dirà anche che lo stato elettromagnetico della materia può essere solo positivo o negativo e si ribadirà che l’esistenza dell’informatica è dovuta alla concezione della matematica binaria e quindi ai due soli numeri 0 e 1 .

A porzioni di materia magnetizzabile con stato elettromagnetico positivo assegnamo il valore 1 mentre alle altre porzioni con stato elettromagnetico negativo assegnamo il valore 0.

Così, diremo, funzionava l’informatica degli albori. I computer erano costituiti da giganteschi anelli metallici collegati da fili. Alcuni anelli erano magnetizzati, altri no. La successione di polarizzazioni dava origine a lunghe sequenze di 1 e di 0 e quindi di dati.

La magnetizzazione era il risultato del passaggio di corrente elettrica che attraversava gli anelli.

I vecchi giganteschi circuiti sono oggi sostituiti dai chip costituiti da sottili lamine di materiale semiconduttore (silicio) che permette di realizzare con le singole molecole il meccanismo di cariche positive e negative, prima realizzato dai grandi circuiti.

Se sono cambiate le dimensioni e le capacità di elaborazione, non è cambiata però la struttura fisica dell’informazione che è sempre costituita da cariche negative e da cariche positive, da 0 e 1.

Si vuole far capire l’analogia che esiste tra la disposizione della limatura di ferro attorno al filo conduttore e la deposizione dell’informazione digitale magnetica su dischi magnetici nei moderni calcolatori.

Si dirà agli/alle allievi/e che i segnali binari magnetici vengono utilizzati non per l'elaborazione dell'informazione digitale ma per la sua memorizzazione.

Si ribadirà che il campo magnetico ha una certa direzione nello spazio generando un polo sud ed un polo nord.

In natura abbiamo la possibilità di costruire piccoli magneti. Essi sono ottenuti usando materiali detti ferromagnetici. Il ferro infatti ha una disposizione degli elettroni che lo fa diventare un piccolo magnete.

Nei dispositivi magnetici digitali abbiamo dei piccoli magneti che vengono fatti orientare in una direzione od in quella opposta. Otteniamo così un segnale binario ed un bit di informazione ad esso associato.

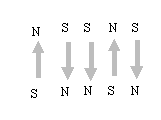
Nei sistemi magnetici digitali è importante la direzione della magnetizzazione.

Una magnetizzazione verso l'alto darà un segnale binario 1, una magnetizzazione verso il basso darà una segnale binario 0.

Si dirà agli/alle allievi/e che alto e basso in realtà non esiste, ma che si tratta di un utile convenzione che ci diamo.

Una testina di lettura riotterrà il segnale elettronico binario originario.

E’ infatti possibile conservare la direzione dei campi magnetici nei materiali ferromagnetici per molti anni. E’ inoltre possibile ottenere la magnetizzazione di zone molto piccole, impaccando così su superfici ridotte una grandissima quantità di informazione.

Nei moderni calcolatori l'informazione digitale magnetica viene depositata su dischi metallici posti in maniera concentrica , uno sull’altro, sullo stesso asse attorno al quale ruotano in continuazione a grande velocità.

Su questi dischi la testina di lettura e di scrittura è libera di muoversi a distanze diverse dal centro del disco percorrendo così cerchi più o meno ampi definiti tracce. Su ogni traccia di un disco vengono memorizzati moltissimi bit. Ogni traccia è poi suddivisa in parti che vengono definiti settori.

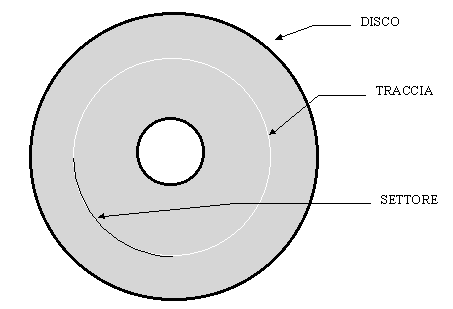
Il settore è un blocco di bit che viene letto o scritto in una singola operazione. Su di un disco non conviene leggere il singolo bit, ma il gruppo di bit compreso in un settore.

I moderni calcolatori utilizzano, dunque, per la memorizzazione dei dati, dischi magnetici impilati in grado di memorizzare i nostri dati.

Lo fanno cambiando il loro stato magnetico fra due stati diversi possibili, che possono rappresentare i valori 0 e 1 e quindi un sistema di codifica dei dati che in precedenza abbiamo detto binario e che consideriamo la base dell'elaborazione automatica dell'informazione.

Si chiede dunque agli/alle allievi/e se, dalla loro esperienza, sono in grado di definire con una parola l’insieme dei dischi magnetici sopra descritti.

Foto 2

Disegno 2


Sicuramente la gran parte di essi/e sarà in grado di definirli con il termine di Hard-disk (foto 2) e di dire a questo punto che ogni parte dell’Hard-disk assume un valore binario.

Qualche studente/studentessa ricorderà anche che il valore binario viene indicato con il termine bit, da binary digit.

Si discuterà quindi dei termini byte, definito come successione di 8 bit che combinati assieme nelle varie configurazioni di 0 e 1 possono dare 28=256 dati differenti, e dei suoi multipli.

Si considereranno i multipli del byte, facendo leva sull’esperienza degli/delle allievi/e.

Si chiederà se ad alcuni/e non sia mai capitato di avere problemi con lo spazio dell’hard disk del proprio PC oppure se nell’acquistare un PC si siano imbattuti in parole quali Gigabyte riferite all’Hard disk.

Vengono definiti i famosi kilobyte, megabyte, gigabyte, terabyte che usualmente vengono rappresentati dalle sigle KByte, MByte,GByte, TByte ecc. o più semplicemente KB, MB, GB, TB.

Si chiederà agli/alle allievi/e il significato che attribuiscono ai prefissi kilo, mega, giga, tera, che hanno già incontrato nello studio del Sistema Internazionale di misura.

La risposta sarà che questi prefissi sono associati rispettivamente a potenze crescenti di 10, cioè 103,106,109,1012 ecc.

A questo punto si riprenderà la scheda Far di conto nel sistema binario e si ricorderà che con i numeri binari si lavora “in base 2” e quindi i multipli sono definiti in termini di potenze di 2.

Viene illustrata la seguente tabella

Multiplo

Sigla

Valore

bit

bit

21=2

byte

Byte

28=256 (8 bit)

kilobyte

KB

210=1024 (byte)

megabyte

MB

220=1048576 (byte)

gigabyte

GB

230 (byte)

terabyte

TB

240 (byte)

 

Per verificare se si sia compresa la differenza tra sistema decimale e sistema binario si propongono agli/alle allieve una serie di esercizi di conversione del tipo:

 

1 m = Km

100 Kg = g

0,3 m = Gm

1 g = Tg

1 byte= MB

3 MB= TB

3 TB= byte

2 byte= bit

 

 

 

FAR DI CONTO NEL SISTEMA BINARIO / SCHEDA

 

Nel sistema decimale, quello che usiamo nella vita quotidiana, le cifre di un numero rappresentano, da destra a sinistra, le unità, le decine, le centinaia, . . .

Ogni cifra indica il numero di volte che compare quella tale potenza in base 10 (10 alla 0 =1, 10 alla 1 = 10, 10 alla 2 = 100, 10 alla 3 = 1000, ...)

 

Ad esempio 4726 significa:

 

6 x
10 alla zero
= 6 x
1
6
2 x
10 alla uno
= 2 x
10
20
7 x
10 alla due
= 7 x
100
700
4 x
10 alla tre
= 4 x
1000
4000
____________________
   
totale
  
4726

 

Lo stesso avviene con i numeri binari , con la differenza che qui si lavora “in base 2”. Così ogni cifra da destra a sinistra rappresenta quante volte compare la potenza 0, la potenza 1, la potenza 2, la potenza 3 ecc. di 2.

 

 

Ecco allora che il numero binario 01101010 significa:

 

0 x
2 alla zero
= 0 x
1
0
1 x
2 alla uno
= 1 x
2
2
0 x
2 alla due
= 0 x
4
0
1 x
2 alla tre
= 1 x
8
8
0 x
2 alla quarta
= 0 x
16
0
1 x
2 alla quinta
= 1 x
32
32
1 x
2 alla sesta
= 1 x
64
64
0 x
2 alla settima
= 0 x
128
0
____________________
   
totale
  
96

 

Scheda tratta da Franco Carlini, Chips & salsa Storie e culture nel mondo digitale, Ed. Il Manifesto

Ritorno all’indice