LE FUNZIONI LOGICHE
NELLA PRATICA QUOTIDIANA
Paolo Nicolao
Istituto Tecnico Industriale "F. Solari" di Tolmezzo
Indice
* Introduzione
* Contesto
* Prerequisiti
* Obiettivi
* Contenuti
* Richiami di logica
* Esempi / indicazioni utilizzabili nei vari argomenti
* Operatori logici in ambito elettrico
* Operatori logici in ambito pneumatico
* Operatori logici in ambito elettronico
* Il concetto di memoria
* La memoria in ambito elettrico
* La memoria in ambito pneumatico
* La memoria in ambito elettronico
* Dalla logica cablata a quella programmata
* Bibliografia
| Documentazione in formato PDF | ||
Nei corsi di informatica di base, ma non necessariamente solo in questo contesto, vengono generalmente introdotte le principali funzioni logiche, in particolare l' AND, l' OR e la NOT. Queste nozioni, all'interno di discipline trasversali ai vari ordini di scuola (ad es. matematica), rappresentano di solito il punto di partenza per ulteriori approfondimenti nell'ambito dell'algebra di Boole oppure, nel caso di istituti ad indirizzo tecnico/ professionale, divengono concetti introduttivi per insegnamenti più specialistici.
I temi in esame risultano il più delle volte alquanto astratti per cui gli studenti faticano a farli propri, offrendo spesso solo riscontri di tipo mnemonico/ripetitivo. Inoltre risulta difficile motivare gli alunni all' apprendimento di nozioni che non trovano immediato riscontro con il loro vissuto quotidiano.
Ciò è ancor più vero qualora questi concetti vengano presentati nelle classi iniziali della scuola secondaria superiore (biennio) od anche, ad un livello concettuale diverso, nelle prime classi di specializzazione delle scuole ad indirizzo tecnico (solitamente terzo anno di corso) o professionale .
Le unità didattiche che vengono proposte nel seguito, cercano di rispondere a queste sollecitazioni offrendo agli allievi esempi di utilizzo pluridisciplinare delle funzioni logiche fondamentali.
La struttura delle unità è di tipo modulare e quindi tale da offrire la possibilità di estrapolare, in funzione delle particolari esigenze didattiche, anche singole parti da contestualizzare in relazione alle caratteristiche della classe a cui ci si rivolge.
Come già accennato nell'introduzione, le unità didattiche presentate si rivolgono a classi del biennio iniziale delle scuole medie superiori nelle quali la disciplina informatica sia parte integrante del curricolo o meglio nelle quali sia stato introdotto il concetto di funzione logica. Esse possono essere anche utilizzate come premessa per un' "area di progetto" nella quale si conti di realizzare alcuni degli esempi proposti.
Nel caso di istituti tecnici industriali o professionali, possono essere utilizzate all'interno delle discipline specifiche di indirizzo, utilizzando però le unità didattiche non inerenti all'indirizzo stesso (ad es. agli elettronici quelle di pneumatica, o di area elettrica. e viceversa). La motivazione di quest'ultima affermazione risiede nella voluta genericità della trattazione che non presenta il grado di approfondimento normalmente richiesto per le discipline specifiche di indirizzo. Le proposte di realizzazione pratica potrebbero essere utilizzate come spunti per attuare "aree di progetto" (o ricercare collegamenti interdisciplinari) avendo ovviamente a disposizione la opportuna attrezzatura.
Sulla base di quanto già illustrato, le unità in oggetto vengono poste in fase temporalmente successiva all'introduzione delle funzioni logiche, che quindi ne divengono prerequisiti fondamentali. Inoltre per una maggior comprensione degli esempi e delle esperienze che verranno successivamente proposte risulta fondamentale la conoscenza di alcuni concetti di fisica di base .
Si richiedono quindi:
Conoscenze
Competenze
Capacità
Per detti requisiti non è prevista alcuna verifica iniziale di tipo formale, essendo dato per scontato che le conoscenze di logica derivino dalle precedenti unità didattiche Invece qualora le conoscenze di fisica, verificate in base ad una veloce indagine a campione, risultassero carenti, esse andranno sanate con appositi richiami, da effettuarsi al momento dell'utilizzo dei concetti stessi.
Gli obiettivi sono i medesimi delle unità didattiche che hanno introdotto il concetto di funzione logica puntando quindi ad un loro rafforzamento grazie alla verifica pratica di dette funzioni. In particolare:
Obiettivi generali
Obiettivi specifici
Nel caso in cui si finalizzino le u.d. (unità didattiche) alla realizzazione di un'area di progetto, andranno aggiunti tra gli obiettivi specifici la costruzione del dispositivo obiettivo del lavoro, unitamente al necessario approfondimento delle conoscenze che da ciò certamente deriverà.
Non sono previste verifiche specifiche in quanto le unità vengono proposte come integrative a quanto previsto per i moduli relativi alle funzioni logiche.
La struttura del modulo è la seguente:
per ognuno dei tre ambiti applicativi verranno esposti esempi applicativi delle tre principali funzioni logiche (AND, OR, NOT) e proposta la realizzazione di almeno un "dispositivo" che le utilizzi. Per quest'ultima attività non è stato quantificato l'impegno orario in quanto esso dipende dalle disponibilità di materiale presente in laboratorio o dalla possibilità di inserirla come spunto per l'area di progetto.
per ognuno degli ambiti applicativi verranno forniti esempi di applicazione di sistemi sequenziali e proposta la realizzazione di almeno un "dispositivo" che li utilizzi.
Anche per quest'ultima attività non viene quantificato l'impegno orario, per gli stessi motivi esposti in precedenza.
Le attività proposte per il laboratorio possono essere effettuate dall'insegnante, in forma dimostrativa o, specie per gli ambiti elettrici ed elettronici, direttamente dagli allievi se i laboratori risultano sufficientemente attrezzati.
Nel caso di utilizzo di tecnologia pneumatica andrà previsto l'uso di appositi pannelli, e relativa attrezzatura, di cui verranno forniti gli estremi in sede di dettaglio.
Si consiglia vivamente di sperimentare, eventualmente in sede di area di progetto, almeno una delle realizzazioni proposte in quanto la verifica pratica risulta essere un fattore estremamente positivo per la comprensione dei concetti teorici.
Di seguito viene fornito uno schema di massima di come potrebbe essere svolta l'attività didattica:
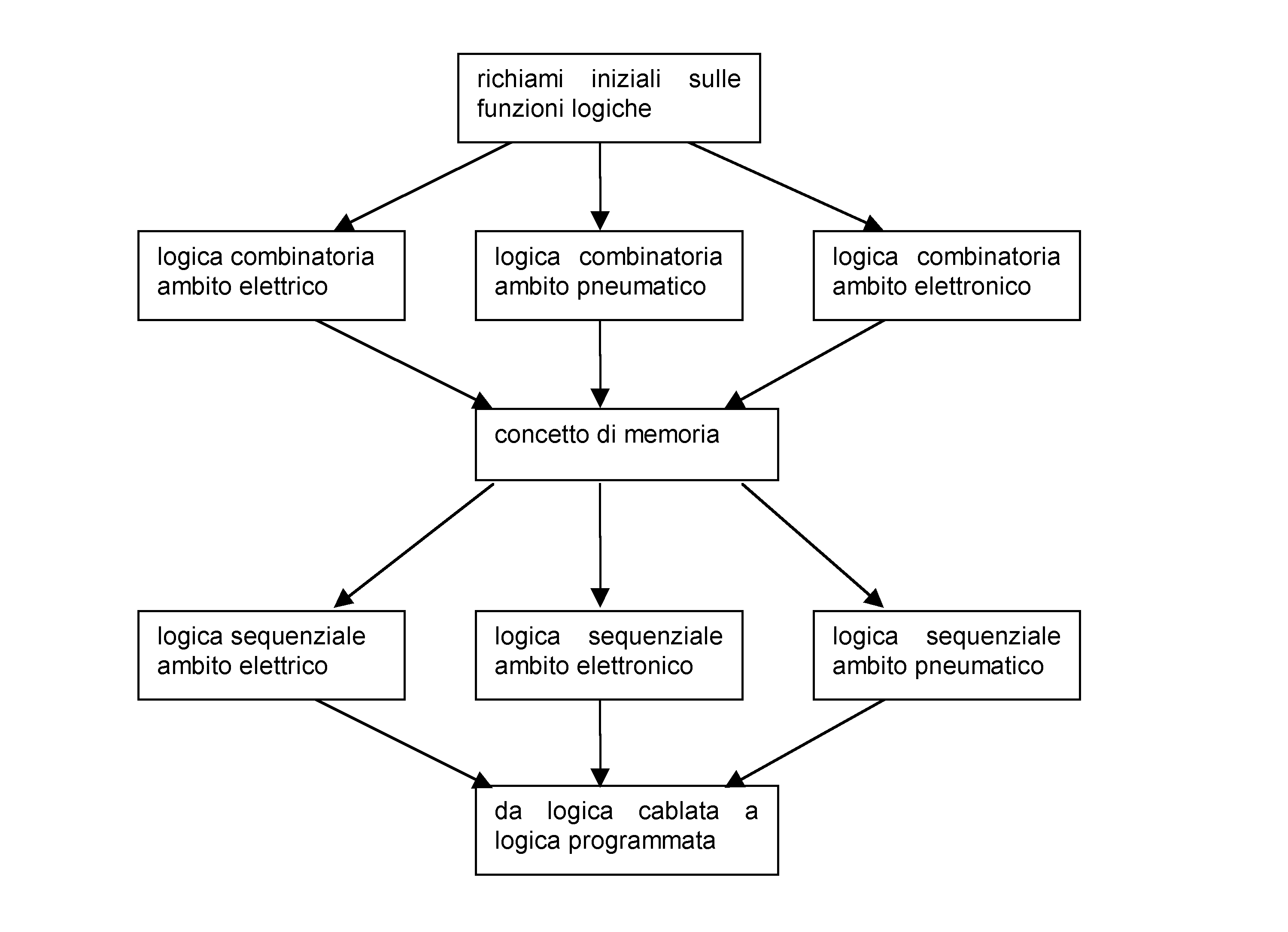
Qualora il tempo a disposizione non sia sufficiente si potrà scegliere anche solo uno degli ambiti proposti.
Si raccomanda comunque di completare in senso verticale l' unità didattica in quanto, essendo l'obiettivo della stessa l'introduzione all'informatica in senso lato, e quindi non solo degli elaboratori elettronici, diventa cruciale illustrare il passaggio dalla logica cablata (cioè dal circuito costruito ad hoc) a quella programmata (cioè l'uso di dispositivi che contengono istruzioni che possono essere facilmente variate o sostituite).
La finalità di questo primo intervento è il richiamo dei temi trattati nelle unità didattiche precedenti, ciò sia per una verifica non formale degli obiettivi delle stesse, sia per consolidarne il raggiungimento.
Questo primo incontro, la cui durata prevista è di circa 2 ore, verrà condotto con metodologia didattica che tenda al massimo coinvolgimento della classe (lezione interattiva o dialogata) per sollecitare dai partecipanti il collegamento dei concetti che si analizzano con la realtà quotidiana, il che rappresenta l'obiettivo principale di questa u.d., e per condurre quella verifica cui si accennava sopra. Ovviamente per alcuni concetti verranno effettuati brevi interventi di tipo frontale (concetti di: misura, operatore logico, etc.), ma essi dovranno essere sempre intercalati da contributi provenienti dalla classe, ovviamente opportunamente sollecitata dall'insegnante. A questo scopo vengono riportati alcuni esempi o indicazioni di massima che dovrebbero facilitare il dialogo insegnante-alunni.
Verranno affrontati i seguenti argomenti
misura di una variabile come rappresentazione della stessa in un particolare istante, variabili continue e variabili discrete
Esempi / indicazioni utilizzabili nei vari argomenti
Misura: La realtà quotidiana offre moltissimi esempi. Alcuni potrebbero essere:
Relazioni tra variabili discrete
|
Posizione |
Posizione selettore |
effetto |
|
1000 |
A |
2 monete da 500 |
|
1000 |
B |
1 moneta da 500 e 5 da 100 |
|
2000 |
A |
4 monete da 500 |
|
2000 |
B |
3 monete da 500 e 5 da 100 |
|
Posizione |
Portiera anteriore |
effetto |
|
A |
Chiusa |
Luce spenta |
|
A |
Aperta |
Luce spenta |
|
B |
Chiusa |
Luce spenta |
|
B |
Aperta |
Luce accesa |
|
C |
Chiusa |
Luce accesa |
|
C |
Aperta |
Luce accesa |
Si tratta della rappresentazione di una variabile binaria con le due posizioni di attivo (ON, 1) o disattivo (OFF, 0). Detta rappresentazione è quella normalmente in uso in ambiente tecnico.
Simboli degli operatori logici
pur in presenza di altre normative, si riportano solo i simboli grafici degli operatori secondo le norme ASA (American Standard Association) che appaiono attualmente le più utilizzate
Si riportano inoltre altri simboli utilizzati nella algebra delle proposizioni per collegare tra loro le variabili in ingresso
La tabella della verità è la seguente:
|
ingresso 1 |
ingresso2 |
uscita |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
il simbolo (ASA) è il seguente
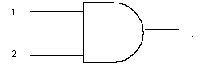
altri simboli: ·, &, Ÿ
La tabella della verità è la seguente:
|
ingresso 1 |
ingresso2 |
uscita |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
il simbolo (ASA) è il seguente
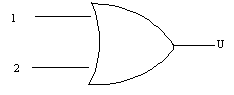
altri simboli: +, |, V
La tabella della verità è la seguente:
|
ingresso |
uscita |
|
0 |
1 |
|
1 |
0 |
il simbolo (ASA) è il seguente
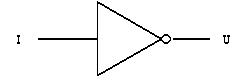
altri simboli: ~, ÿ, ` (trattino che sovrasta la variabile oggetto di negazione)
Funzioni logiche pluriingresso
Per funzioni logiche pluriingresso si intendono quelle funzioni AND o OR che presentano più di due grandezze in ingresso. Le relazioni tra le stesse sono le naturali generalizzazioni di quelle viste in precedenza, cioè:
and darà risposta 1 quando tutti gli ingressi saranno uguali a 1
or darà risposta 0 quando tutti gli ingressi saranno uguali a 0
La metodologia da adottarsi per passare dalla tabella della verità alla sua rappresentazione con funzioni logiche esula dallo scopo di questa unità didattica. Si fornirà quindi sono una tecnica per passare (anche se non ottimizzando) dalla tabella della verità ad uno schema che la rappresenta e che potrà poi essere eventualmente costruito durante una esperienza di laboratorio. La trattazione della mappe di Karnaugh, che racchiudono al loro interno i teoremi dell'algebra di Boole, potrà eventualmente essere affrontata in sede di approfondimento utilizzando la bibliografia sul tema.
La tecnica prevede la costruzione di una tabella per ogni variabile di uscita con un numero di colonne pari a quello degli ingressi. Nelle righe si inseriscono le composizioni dei valori degli ingressi (una per riga) che forniscono un'uscita valida (cioè pari a 1).
Lo schema finale (anche se non ottimizzato) si ottiene ponendo tra loro in OR le grandezze uscenti dalle composizioni degli ingressi presenti nelle singole righe (ci saranno un operatore OR con un numero di ingressi pari al numero di righe). La singola riga verrà rappresentata da un operatore AND che prevede in input tutti gli ingressi eventualmente negando (operatore not) quelli che presentano nella combinazione il valore 0.
La rappresentazione degli schemi è stata ottenuta usando il package Labview˘ della National Instruments qui utilizzato solo per simulazione. La simbologia non è quella prevista dalle norme precedentemente citate ma è ugualmente funzionale a quanto si vuole ottenere. In particolare le variabili binarie sono rappresentate con il simbolo
![]()
in cui T (True- vero) rappresenta il valore 1 e F (false-falso) quello 0.
In un Consiglio di Amministrazione composto da 4 persone viene installato un sistema di votazione elettronico mediante interruttori (interruttore premuto, cioè voto favorevole, variabile = 1). Si vuole determinare uno schema logico che accenda una luce (uscita = 1) nel caso che i voti favorevoli espressi siano in maggioranza
|
consigliere A |
consigliere B |
consigliere C |
consigliere D |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
0 |
lo schema logico sarà il seguente
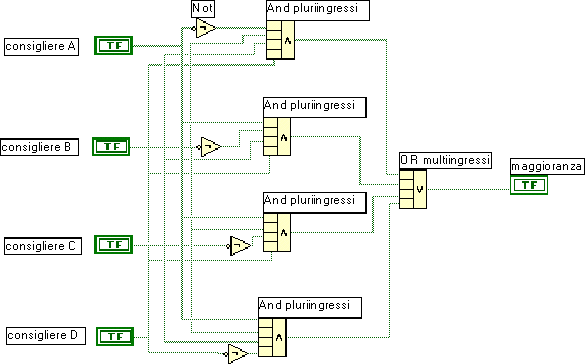
L'esempio si presta ad illustrare sia il concetto di operatore logico pluriingresso, sia a verificare la tecnica per passare dalla tabella della verità allo schema logico.
esempio 2
Un nastro trasportatore è posto in movimento da due motori comandati, tramite opportune interfaccie di potenza ed un circuito combinatorio, da tre interruttori. Di questi uno (A) permette il movimento in avanti, uno (B) quello all'indietro ed uno, di emergenza (C), viene utilizzato per la fermata del nastro. Non è ovviamente ammesso il funzionamento contemporaneo dei due motori.
tabella della verità per il motore A
|
interruttore A |
interruttore B |
interruttore C |
|
1 |
0 |
0 |
tabella della verità per il motore B
|
interruttore A |
interruttore B |
interruttore C |
|
0 |
1 |
0 |
lo schema logico sarà il seguente
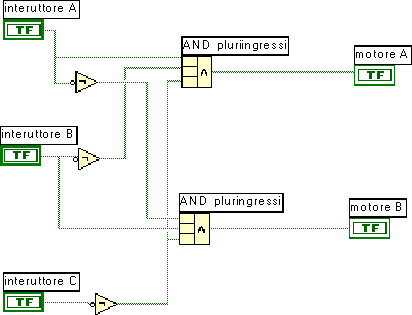
L'esempio si presta ad illustrare la necessità di una tabella della verità per ogni variabile di uscita
| Continua |