La scrittura e i sistemi di numerazione

La scrittura dei numeri ha posto per molti secoli il problema di individuare una rappresentazione comoda ed efficace per i numeri. Presso le civiltà antiche sono stati utilizzati diversi tipi di notazioni, talvolta molto diverse tra loro e dal sistema attualmente adottato. I primi sistemi di numerazione furono per lo più di tipo additivo fondati sull'uso di una qualche base. Le origini dell'attuale sistema di numerazione, il sistema posizionale decimale, non sono del tutto chiare. Gli studiosi concordano comunque sul fatto che furono gli indiani, forse nel VI sec. d.C., ad ideare il sistema di numerazione decimale posizionale. Oggi noi siamo così abituati a questo sistema da non renderci conto della sua immensa importanza nel facilitare le operazioni. L'introduzione del sistema decimale si può considerare un’autentica rivoluzione, per certi versi confrontabile all'attuale introduzione del computer.

Fig. 12. Ricostruzione di una tavoletta sumera in terracotta contenente alcuni valori numerici. La scrittura costituisce uno dei primi ausili sfruttati per eseguire calcoli di importanza fondamentale. Annoverare la scrittura tra gli strumenti di calcolo può sembrare una cosa strana, data l'enorme versatilità di questo strumento. La scrittura costituisce infatti uno strumento universale per pensare, per registrare e per trasmettere informazioni di qualunque natura. Questo mezzo si è rivelato essenziale anche nell'ambito del calcolo. Nei secoli sono stati utilizzati svariati tipi di supporti: dalle tavolette di argilla a quelle di cera, dal papiro alla pergamena, dalla lavagna alla carta.

Fig. 13. Carta e penna usati per attività di calcolo. Fino al 1800 la carta è stata un supporto per la scrittura abbastanza costoso, il cui uso per l'attività di calcolo era limitato. Per tale ragione, per lungo tempo in Europa è continuato l'uso dell'abaco e delle taglie.

>

(a) sistema di numerazione egizio.

(b) sistema di numerazione greco

(c) sistema di numerazione romano

Fig. 14 a, b, c. Alcuni sistemi di numerazione antichi. La scrittura dei numeri ha posto per molti secoli il problema di individuare una rappresentazione comoda ed efficace per i numeri. Presso le civiltà antiche sono stati utilizzati diversi tipi di notazioni, talvolta molto diverse tra loro e dal sistema attualmente adottato. I primi sistemi di numerazione furono per lo più di tipo additivo fondati sull'uso di una qualche base. In questi sistemi, ad ogni simbolo di un dato tipo è associato un valore numerico prefissato, e il sistema si dice additivo perché il valore del numero rappresentato si ottiene sommando i valori numerici dei singoli simboli che costituiscono la scrittura del numero.

Fig. 15. Codex Vigilanus: viene considerato il più antico testo europeo contenente le nostre cifre decimali (risale al 976 d.C.). Si nota che ancora non compare un simbolo per rappresentare lo zero. Il nostro sistema di numerazione è un sistema di tipo posizionale in quanto il valore numerico associato ad ogni cifra varia secondo la posizione che essa occupa nella scrittura del numero. Le origini dell'attuale sistema di numerazione, il sistema posizionale decimale, non sono del tutto chiare. Gli studiosi concordano comunque sul fatto che furono gli indiani, forse nel VI sec. d.C., ad ideare il sistema di numerazione decimale posizionale, che fu trasmesso in Europa dagli arabi. Fu probabilmente l'abaco a suggerire agli indiani il sistema posizionale. Per indicare le righe prive di sassolini, gli indiani pensarono di usare un puntino, così come noi oggi usiamo lo zero. In Europa, tra i personaggi che maggiormente contribuirono ad introdurre il nuovo sistema di numerazione decimale attorno al XIII sec. d.C. va sicuramente menzionato Leonardo Pisano (1170-1250), detto Fibonacci. Con il suo Liber Abaci (1228) presentò il sistema posizionale con gli algoritmi per le operazioni evidenziando i notevoli vantaggi del metodo.

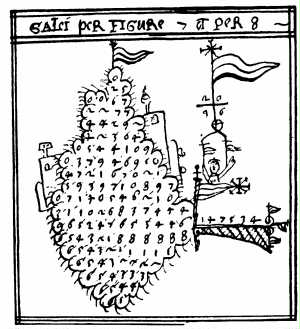
Fig. 16. La divisione secondo il metodo "per galera", derivata da quella con l'abaco (utilizzata fino a secolo XV). La numerazione posizionale comportò non solo l'introduzione di un nuovo sistema di scrittura dei numeri, ma determinò parallelamente l'introduzione delle regole di calcolo che noi oggi utilizziamo per eseguire le quattro operazioni. Per un certo periodo l’abaco e i nuovi metodi di calcolo basato sul sistema decimale rivaleggiarono, come testimoniato da vari illustrazioni del tempo. L'introduzione del sistema decimale posizionale, che implica l'impiego dello zero, si può considerare un’autentica rivoluzione. Noi oggi siamo così abituati a questo sistema da non renderci conto della sua immensa importanza nel facilitare le operazioni. E' sufficiente provare ad effettuare una moltiplicazione o una divisione nella numerazione romana, magari con quantità non intere, per rendersi conto delle difficoltà che sorgono nei sistemi pre-posizionali.

------------------
|       4253 x   |
|       7689 =   |
|  -----------   |
|      38277     |
|     34024      |
|    25518       |
|   29771        |
|  -----------   |
|   32701317     |
------------------

------------------
|      42,53 x   |
|      7,689 =   |
|  -----------   |
|      38277     |
|     34024      |
|    25518       |
|   29771        |
|  -----------   |
|  327,01317     |
------------------

Fig. 17. La notazione posizionale e la virgola decimale facilitano notevolmente le operazioni con i numeri non interi. L'introduzione della virgola e delle cifre decimali permise di raffinare il sistema decimale per la rappresentazione di quantità non intere rendendolo ancora più vantaggioso rispetto agli altri metodi. La moltiplicazione di 42,53 e 7,689 non è essenzialmente più difficile della moltiplicazione dei numeri interi 4253 e 7689, poiché, a parte la gestione della virgola, vengono utilizzati i medesimi procedimenti di calcolo. I primi documenti che evidenziano l'impiego della virgola sono De planis triangulis (1592) di Giovanni Antonio Magini (1555-1617), un astronomo amico di Keplero e una tavola dei seni (1593) di Cristoforo Clavio (1537-1612), un gesuita amico di Keplero.